MATLAB实现的热电偶动态补偿实验解析

“热电偶动态补偿实验（matlab 程序）” 热电偶动态补偿实验是一种基于MATLAB的实践教学活动，旨在深入理解动态测量原理和热电偶的特性。实验中，通过使用K型热电偶、数采卡、应变放大器等设备，模拟一阶系统的响应，分析热电偶的时间常数，并设计补偿电路以优化系统性能。 实验的核心在于热电偶，这是一种常用的温度传感器，由两种不同金属材料焊接而成。当两端存在温差时，会产生电动势，即热电势，可用于测量温度。在本实验中，热电偶被快速放入热水中，产生近似的阶跃输入，这样可以观察和分析其响应时间，进而确定时间常数。 实验设备包括K型热电偶、PCI-6013型数采卡（由美国国家仪器公司生产）、YE3817型应变放大器（来自江苏联能电子技术有限公司），以及相关电子元件。YE3817型应变放大器作为电压放大器，将热电偶产生的微弱信号放大，然后通过数采卡送入计算机进行数据采集。实验步骤包括设置桥盒连接、信号放大、数据采集和补偿电路的添加。 实验步骤详细说明如下： 1. 首先，将热电偶接入YE29003A型桥盒，再通过应变放大器进行电压放大，接着通过PCI-6013型数采卡以1kHz的采样率将信号送入上位机（电脑）。 2. 然后，将热电偶快速放入热水中，记录其响应，待输出稳定后停止采集并保存数据。之后，让热电偶冷却至室温。 3. 在补偿阶段，会在应变放大器的输出端和数采卡之间添加补偿电路，再次重复实验步骤，对比补偿前后的响应差异。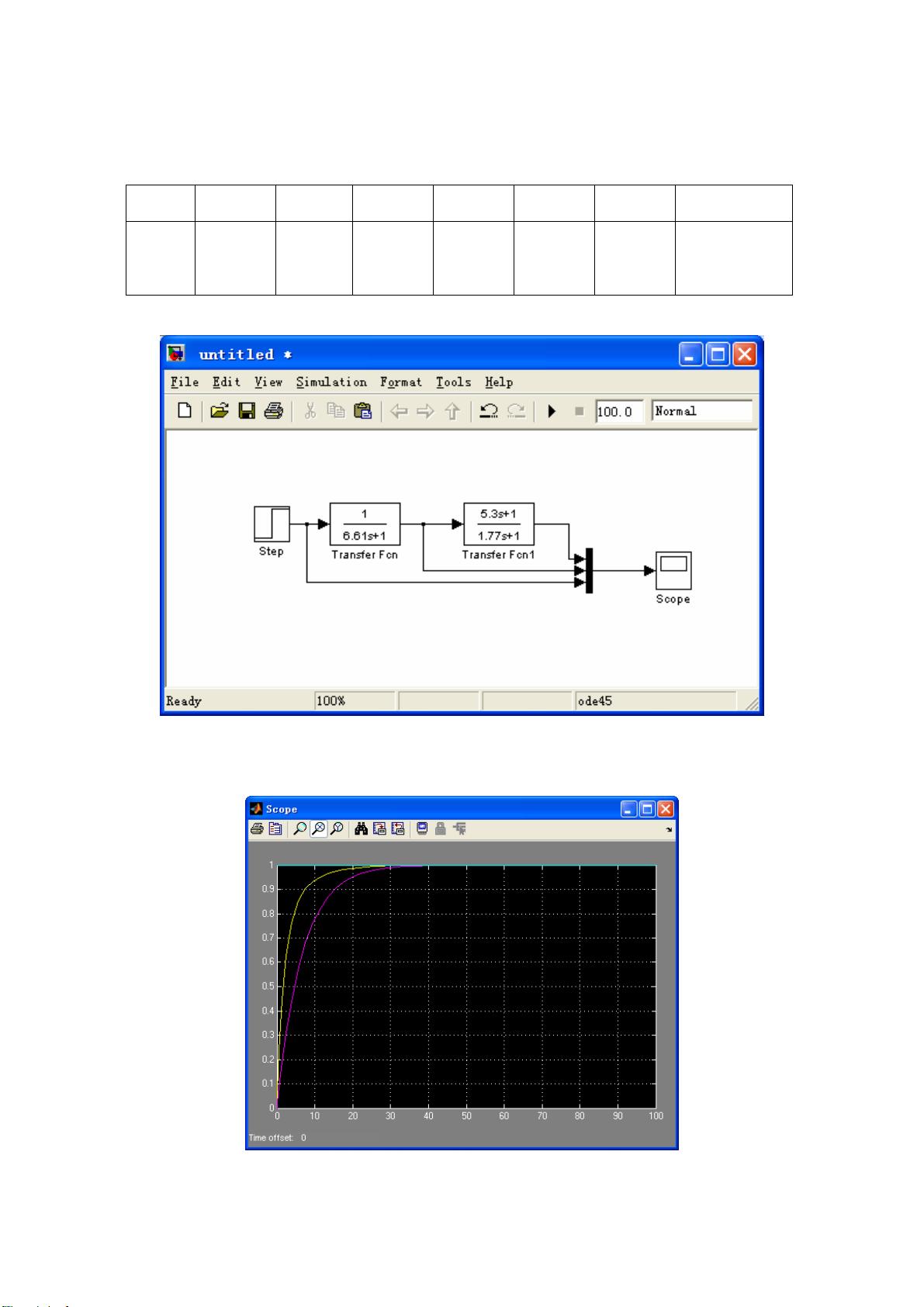 实验数据的分析主要包括热电偶的阶跃响应曲线，这些曲线展示了不同情况下热电偶的输出变化。通过对这些曲线的分析，可以计算出时间常数，进而评估系统的一阶特性。例如，热电偶1在不同条件下的时间常数计算结果可能略有差异，但总体保持一致，证明系统为一阶系统。根据这些时间常数，可以设计补偿环节来减小时间常数，提高系统的响应速度和带宽。 实验中提到的传递函数表示为 () 6.61 1 k Hs s = + ，其中6.61代表原始时间常数，通过引入适当的补偿环节（例如RC网络）可以调整这个常数，使得系统响应更快。MATLAB程序在这个过程中起到了关键作用，它用于模拟和分析补偿电路的效果，优化系统性能，使得热电偶的动态响应更加准确和快速。 这个实验是一个结合理论与实践的教学案例，通过实际操作让学生理解热电偶的工作原理，掌握动态测量中的时间常数概念，以及如何通过补偿电路改进系统性能。此外，实验也强调了MATLAB在信号处理和系统分析中的应用，提升了学生在实际工程问题中的解决能力。