多视图语义与局部保持相关投影

131 浏览量更新于2024-08-26 收藏 400KB PDF 举报

"语义和位置相关性投影是一种多视图关联学习方法，旨在利用内在视图和间视图的角度同时寻找语义公共子空间。该方法由Yan Hua、Jianhe Du、Yujia Zhu和Ping Shi等人提出，主要用于解决异质数据中的多视图关联分析问题。传统的方法如典型相关分析（CCA）及其变种通常只关注视图间一对一对应的相关性，但往往忽略了每个视图数据的判别性多标签信息和局部结构。SLPCP（多标签语义和局部保持相关投影）则填补了这一空白。 SLPCP方法的核心在于通过联合学习视图特异性的线性投影，来捕获数据的语义信息和局部结构。这一过程可以通过广义特征值分解轻松优化，通过连接多个视图的投影实现。在实际应用中，SLPCP被应用于图像和文本数据的检索任务，显示了其在保留数据语义和位置相关性方面的优势。在多视图学习中，每个视图可以视为数据的不同表示或维度，例如，对于图像和文本数据，图像可能是颜色、纹理等视觉特征的表示，而文本则可能是关键词或主题的表示。SLPCP的目标是找到一个公共的空间，在这个空间中，不同视图的数据能保持它们的语义相关性，同时保持各自的局部结构，比如图像中的物体区域或文本中的主题群组。 SLPCP的优化策略基于广义特征值分解，这是一种有效的数学工具，用于找出矩阵对之间的关系，特别适合处理多视图数据的线性变换问题。通过这种方式，SLPCP能够发现潜在的语义相关性和局部结构，并在投影过程中尽可能地保留这些特性。在实验部分，SLPCP可能与其他多视图学习方法进行了对比，以证明其在图像和文本检索任务上的性能提升。这些实验可能包括定量评估（如精度、召回率等指标）和定性分析（如可视化结果），以展示SLPCP如何在维持高相关性的同时，捕捉到数据的复杂性。 SLPCP是一个创新的多视图学习算法，它结合了语义信息和局部结构的保持，对于处理和分析多元异构数据提供了新的途径，尤其在信息检索和数据分析领域具有广泛的应用前景。"

SEMANTICS AND LOCALITY PRESERVING CORRELATION PROJECTIONS

Yan Hua

∗

, Jianhe Du

∗

, Yujia Zhu

†

, Ping Shi

∗

Information Engineering School, Communication University of China, huayan@cuc.edu.cn

†

National Engineering Lab for Information Security Technologies, Institute of Information Engineering, CAS

ABSTRACT

Multi-view correlation learning has attracted great attention

with the proliferation of heterogeneous data. Typical method-

s, such as Canonical Correlation Analysis (CCA) and its vari-

ants, usually maximize one-to-one corresponding correlation

of inter-view data, while most of them neglect discriminative

multi-label information and local structure of each view data.

In this paper, we propose multi-label Semantics and Locality

Preserving Correlation Projections method (SLPCP), which

seeks for a semantic common subspace by jointly learning

view-speciﬁc linear projections from intra-view and inter-

view perspectives simultaneously. SLPCP can be easily op-

timized with generalized eigenvalue decomposition via con-

catenating the projections of multi-views. Applied to retrieval

tasks of image and text data in experiments, SLPCP outper-

forms state-of-the-art methods on a widely used dataset NUS-

WIDE. The extensive experiments also validate that it is ef-

fective to preserve the multi-label semantics and locality of

multi-view data.

Index Terms— Correlation learning, Multi-label, Inter-

view, Intra-view, Image and text retrieval

1. INTRODUCTION

Different types of contents from heterogeneous view or

modality could describe relevant topics, for example, images

and their surrounding texts on web pages, faces captured at

different poses and sentences of multilingual language. Ac-

quiring useful information from multi-view data can promote

the applications in computer vision and multimedia ﬁeld [1]

[2] [3]. In the recent decade, considerable work [4] [5] has

been conducted along with the rapidly increasing multi-view

data and application demands.

Most of previous work focuses on learning a common

subspace shared by multi-view data, in which different types

of data can be directly compared. The most typical method is

Canonical Correlation Analysis (CCA) [6] [1]. The subspace

methods learn the comparable representations by maximiz-

ing the correlations [6] [7] or minimizing the distances [8]

The work is supported by the National Natural Science Foundation of

China (Grant No.61601414), and supported by SAPPRFT Project (No. 2015-

17).

Multi-label: glacier, mountain,

nighttime, person, sign, sky,

sun, sunset

Multi-label: mountain, sky,

sunset

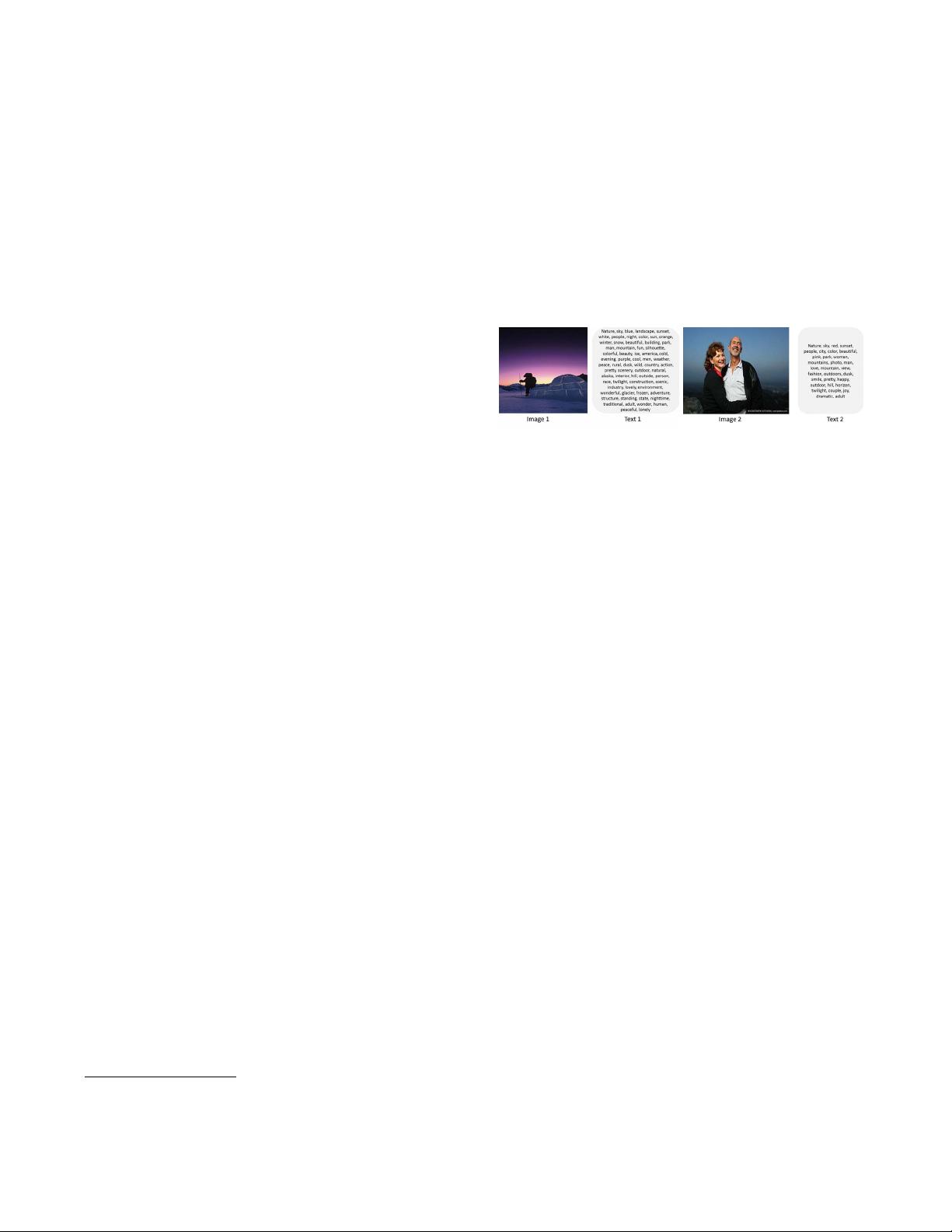
Fig. 1. Two pairwise multi-view samples with multi-labels

from NUS-WIDE dataset. The two views are image and text,

respectively.

of coupled multi-view samples. Though they could narrow

the gap between heterogeneous data by modeling one-to-one

inter-view correlation, they are not designed to utilize class

information to learn discriminative subspace. Single class in-

formation of multi-view samples is introduced in discrimi-

native common subspace learning methods [3] [9] [10] [11].

Recently, three-view CCA [2] and multi-label CCA [12] are

proposed to build the inter-view correlation with multi-labels.

However, multi-label semantics existed in multi-view data in-

volve the semantics not only in inter-view but also in intra-

view data. For example, two multi-view pairs from NUS-

WIDE dataset shown in Fig.1, the left pair is annotated with

labels “glacier, mountain, nighttime, person, sign, sky, sun,

sunset” and the right pair with “mountain, sky, sunset”. The

multi-label information is not only shared between the inter-

view samples (Image 1 vs. Text 1, Image 1 vs. Text 2, Image

2 vs. Text 1 and Image 2 vs. Text 2), but also between intra-

view samples (Image 1 vs. Image 2 and Text 1 vs. Text 2).

In this paper, we introduce a semantics preserving correlation

method which could model multi-label information from both

inter-view and intra-view perspectives.

Most existing methods [8] [12] [3] are linear methods

by learning globally linear transformations for heterogeneous

multi-view data. To deal with non-linear correlations, almost

all subspace learning methods could be extended to kernel

version, where the non-linear problem is transformed into an-

other more possibly linear one in high dimensional (even in-

ﬁnite) feature space with kernel function. However, they still

978-1-5090-6067-2/17/$31.00

2017 IEEE

Proceedings of the IEEE International Conference on Multimedia and Expo (ICME) 2017 10-14 July 2017

913

下载后可阅读完整内容，剩余5页未读，立即下载

weixin_38571603

粉丝: 3
资源: 925

多视图语义与局部保持相关投影

基于语义自编码哈希学习的跨模态检索方法.docx

浅层语义索引

cmrf:跨媒体相关性融合的图像检索

自适应分层语义聚合的跨模态相关学习

基于模糊集的主题提取和层次发现算法 (2007年)

基于局部敏感哈希算法和神经网络学习的跨媒体检索方法.pdf

论文研究-基于矩阵分解和子模最大化的微博新闻摘要方法.pdf

语义自编码哈希提升跨模态检索效率与深度关联

深度学习结构化语义模型在点击数据驱动的网络搜索中的应用

机器学习中的线性相关性：特征选择与降维的应用场景

最新资源