线性化系统分析与设计中的优化方法

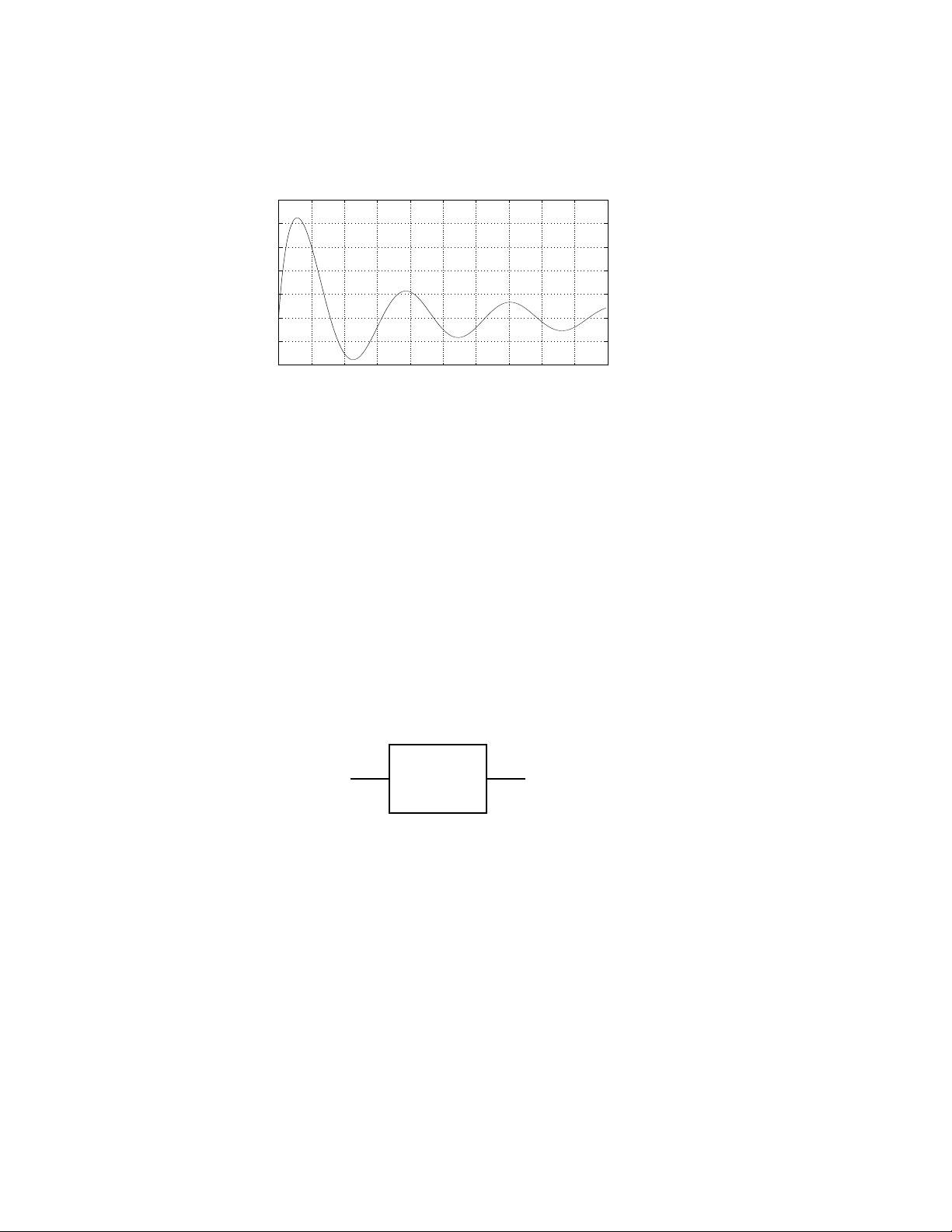
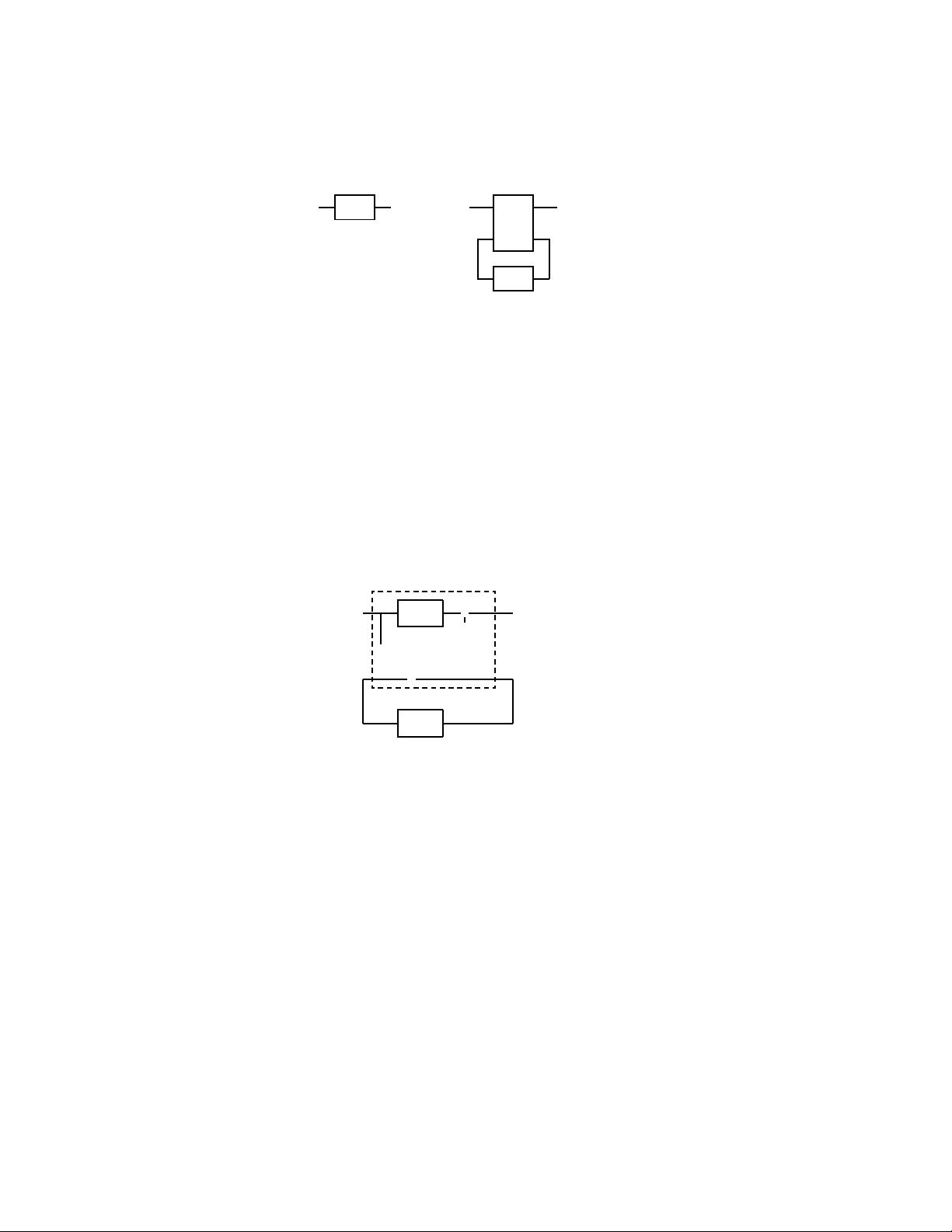
“Optimization Methods in Analysis and Design of Linearized Systems”是一本深入探讨非线性系统线性化及其优化设计的著作，书中包含MATLAB源代码。本书主要关注如何通过线性化技术对非线性系统进行分析和设计，并利用优化方法提升控制性能。 1. 引言 - 动机示例 - 带有延迟控制的倒立摆：这个例子展示了非线性系统中的延迟如何影响系统的稳定性，以及线性化在解决此类问题中的应用。 - 高效的多输入多输出（MIMO）稳定：讨论了如何通过线性化和优化来实现MIMO系统的高效稳定，提高系统性能。 - 讲座结构 - 系统及其近似：介绍如何对非线性系统进行线性化处理，以便进行分析和设计。 - 显式优化线性系统：阐述如何直接对线性化后的系统进行优化，以达到特定的设计目标。 - 凸优化与鲁棒性分析：讨论如何利用凸优化技术来增强系统的稳健性，对抗不确定性。 2. 系统模型 - 一般系统 - 信号：定义和理解系统中的信号类型和特性。 - 行为模型：探讨基于系统行为的建模方法，不依赖于特定的内部表示。 - L2功率增益：衡量系统输出相对于输入的波动程度。 - 系统的外层近似：如何构建系统特性的外部边界，用于分析和设计。 - 小增益定理：用于判断多个子系统交互时的整体稳定性。 - 传递矩阵模型的LTI系统 - 拉普拉斯变换和连续时间傅里叶变换：作为分析LTI系统的基础工具。 - 连续时间系统的传递矩阵模型：详细描述这种模型的构建和特性。 - H-无穷范数：衡量系统在所有可能输入下的最大增益，用于鲁棒控制设计。 - 传递矩阵模型的L2增益：衡量系统在L2空间内的响应强度。 - 传递矩阵模型的外层近似：扩展模型的表示，以包括更广泛的系统行为。 - 状态空间模型 - LTI模型的状态空间定义：解释状态变量的选择和模型的构建。 - 可控性和可观测性：讨论系统能否通过输入和输出来完全控制和观察其状态的重要性。 - 状态空间模型的L2增益：基于状态空间模型评估系统对扰动的敏感性。 这本书全面涵盖了线性化系统分析和设计的关键概念，包括非线性系统的线性化、系统模型的建立以及如何运用优化方法来改善系统性能。MATLAB源代码的提供使得读者能够实际操作和理解理论知识，对于学习和研究控制系统设计的工程师和学者来说是一份宝贵的资源。