Python机器学习中的线性代数基础教程
需积分: 5 114 浏览量
更新于2024-06-16
收藏 9.9MB PDF 举报
"这篇资源是一个关于机器学习所需的线性代数知识的英文教程,通过Python进行讲解,适合希望在机器学习领域应用线性代数基础知识的学习者。教程旨在提供一个实用的线性代数入门,帮助理解机器学习模型背后的数学原理。"
在机器学习中,线性代数扮演着至关重要的角色,它是构建和理解众多算法的基础。以下是一些关键的线性代数概念及其在机器学习中的应用:
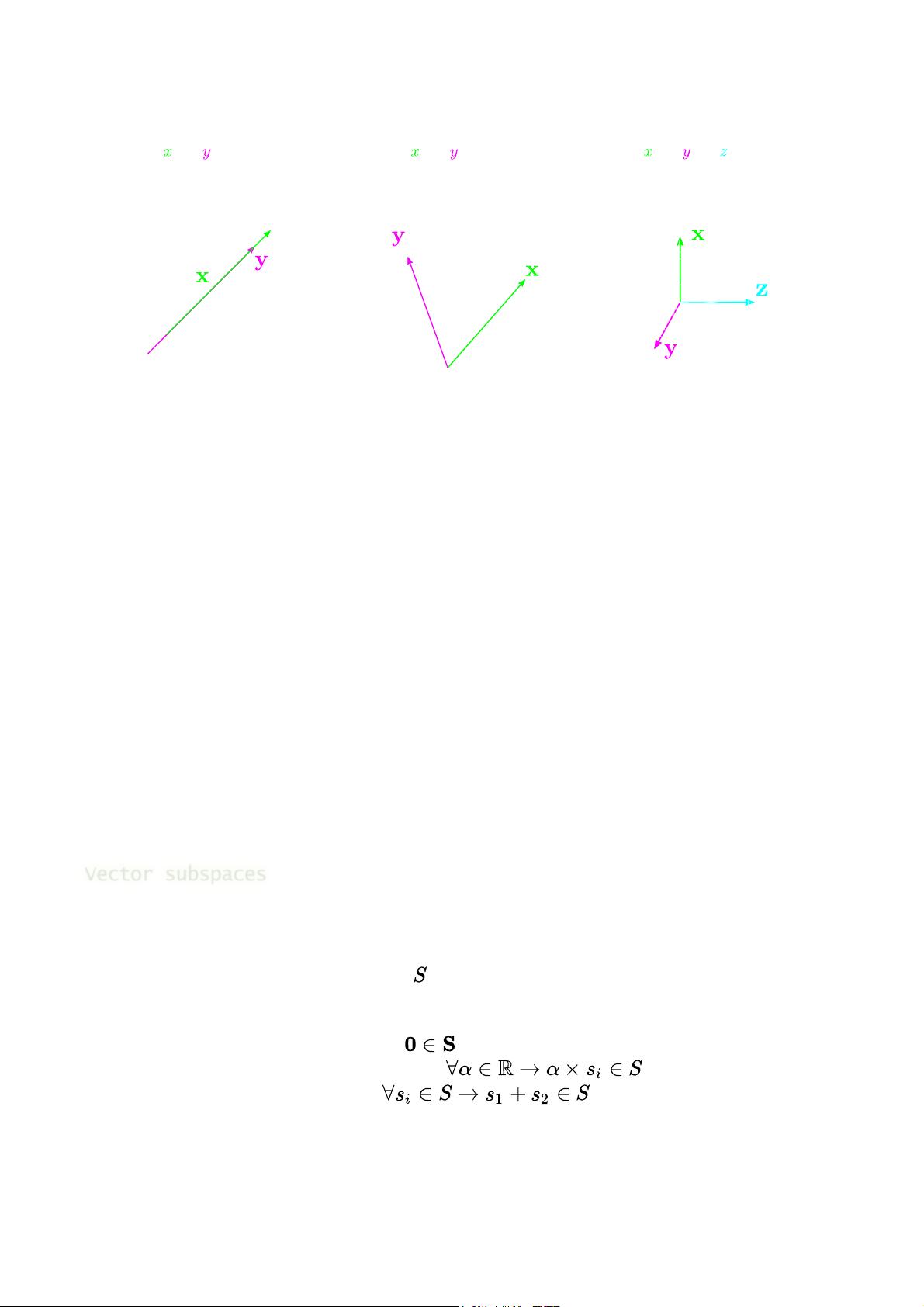
1. 向量(Vector):向量是包含数值的有序数组,可以表示数据点或特征。在机器学习中,向量常用于表示样本的特征,如图像的像素强度、文本的词频等。
2. 矩阵(Matrix):矩阵是由多个数值构成的矩形阵列,可以表示多个变量之间的关系。在机器学习中,矩阵广泛用于数据转换、特征缩放、线性回归、PCA(主成分分析)等。
3. 线性组合(Linear Combination):向量可以通过线性组合得到,即用一组基向量的标量乘积相加。在机器学习中,这用于理解数据的表示空间,如神经网络中的权重更新。
4. 线性变换(Linear Transformation):通过矩阵乘法实现,将一个向量空间转换为另一个向量空间。在机器学习中,这可以用于特征提取、图像旋转和平移等。
5. 奇异值分解(Singular Value Decomposition, SVD):这是一种将矩阵分解为三个矩阵乘积的方法,常用于降维、推荐系统和图像处理。
6. 特征值与特征向量(Eigenvalues and Eigenvectors):当矩阵乘以其特征向量时,结果只是特征向量乘以相应的特征值。在机器学习中,这用于主成分分析、谱聚类和稳定性分析。
7. 正交性(Orthogonality):如果两个向量的内积为零,则它们正交。在机器学习中,正交基可以用于无损地表示数据,例如PCA中的主成分。
8. 行列式(Determinant)和逆矩阵(Inverse Matrix):行列式用于判断矩阵是否可逆,逆矩阵则用于解决线性方程组。在机器学习中,这些用于求解权重矩阵和计算条件数,以评估模型的稳定性。
9. 最小二乘法(Least Squares):在过完备数据集上寻找最佳拟合线的方法,广泛应用于线性回归问题。
10. 核方法(Kernel Methods):如支持向量机(SVM),利用核函数将数据映射到高维空间,实现非线性分类和回归。
通过Python,学习者可以更直观地理解和操作这些概念,从而更好地应用于实际的机器学习项目。这个教程涵盖了线性代数的基础,对于初学者来说是一个良好的起点,能够为更深入的机器学习学习打下坚实的基础。
2022-12-07 上传
2024-06-17 上传
2019-07-19 上传
2024-11-14 上传
2022-05-06 上传
2021-05-30 上传
大吉大利都吃鸡
- 粉丝: 567
- 资源: 4
最新资源
- JavaScript实现的高效pomodoro时钟教程
- CMake 3.25.3版本发布:程序员必备构建工具
- 直流无刷电机控制技术项目源码集合
- Ak Kamal电子安全客户端加载器-CRX插件介绍
- 揭露流氓软件:月息背后的秘密
- 京东自动抢购茅台脚本指南:如何设置eid与fp参数
- 动态格式化Matlab轴刻度标签 - ticklabelformat实用教程
- DSTUHack2021后端接口与Go语言实现解析
- CMake 3.25.2版本Linux软件包发布
- Node.js网络数据抓取技术深入解析
- QRSorteios-crx扩展:优化税务文件扫描流程
- 掌握JavaScript中的算法技巧
- Rails+React打造MF员工租房解决方案
- Utsanjan:自学成才的UI/UX设计师与技术博客作者
- CMake 3.25.2版本发布,支持Windows x86_64架构
- AR_RENTAL平台:HTML技术在增强现实领域的应用