理解支持向量机：从线性到非线性

"本文是基于李航的《统计学习方法》对支持向量机(SVM)的总结，涵盖了从线性可分到非线性情况的SVM理论，包括硬间隔最大化、软间隔最大化和使用核函数处理非线性问题。" 支持向量机(SVM)是一种强大的监督学习算法，尤其在分类任务中表现优异。它主要通过找到一个最优的决策边界（即分离超平面）来最大化类别之间的间隔，从而实现对样本的有效分类。 1. **训练数据与线性可分支持向量机**： 在训练数据线性可分的情况下，SVM的目标是找到一个能够最大程度分离两类样本的超平面。这可以通过**硬间隔最大化**来实现，即寻找一个能够使所有样本点都位于间隔边界之外的超平面。 2. **软间隔最大化**： 当数据不是完全线性可分时，SVM引入了**软间隔**的概念，允许一部分样本点落在间隔内，通过引入惩罚项来平衡分类的准确性和间隔的大小。 3. **线性不可分情况下的非线性支持向量机**： 对于非线性数据，SVM通过引入**核函数**将低维空间的非线性问题转换到高维空间中的线性问题，如径向基函数(RBF)核、多项式核等，从而实现非线性分类。 4. **函数间隔与几何间隔**： SVM中，**函数间隔**衡量的是样本点到超平面的直线距离，而**几何间隔**则是考虑了超平面的单位长度后的实际距离。两者的关系是，几何间隔是函数间隔的标准化形式，总是非负且不会超过函数间隔。 5. **最大间隔分离超平面的优化问题**： SVM的目标是找到最大化几何间隔的超平面，这可以转化为一个凸二次规划问题。在约束条件下，确保所有样本点的几何间隔最小值大于等于1，从而保证了分类的鲁棒性。 6. **存在唯一性**： 如果训练数据集线性可分，那么存在且仅有一个最大间隔的分离超平面，这是因为间隔最大化问题具有唯一解。 7. **支持向量**： 支持向量是在训练数据集中离决策边界最近的样本点，它们决定了间隔的大小和超平面的位置，因此得名。 8. 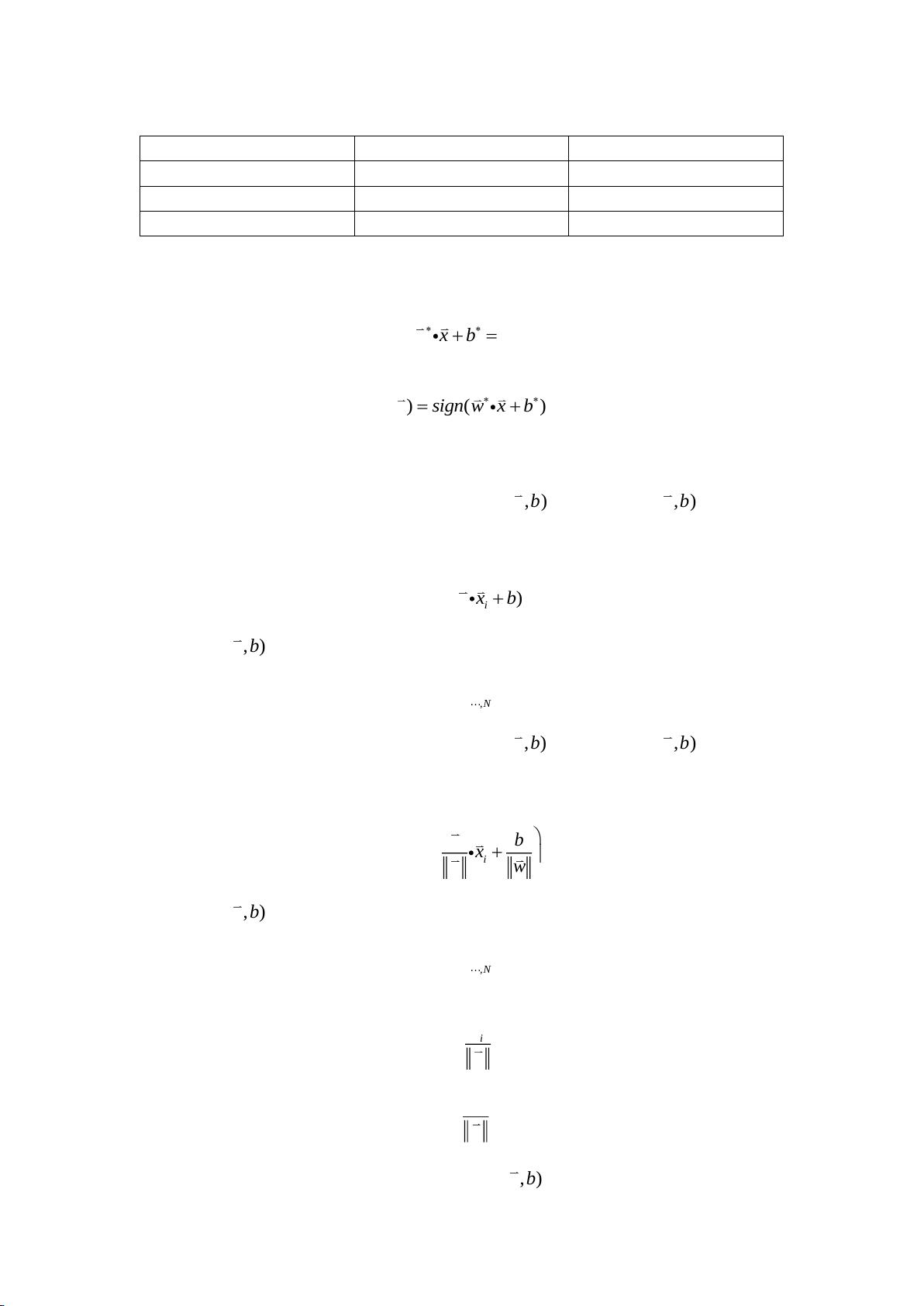**分类决策函数**： SVM的分类决策函数通常表示为`sign(w·x + b)`，其中`w`是权重向量，`x`是输入样本，`b`是偏置项，`sign`函数决定样本的分类。 通过理解和支持向量机的核心概念，我们可以有效地应用于实际问题，解决各种复杂的分类任务。在实际应用中，选择合适的核函数和调整正则化参数（如C）对于模型的性能至关重要。同时，SVM也常用于回归任务，即支持向量回归(SVR)。尽管SVM在大数据集上可能较慢，但其出色的泛化能力和理论基础使其在许多领域中仍然是一种重要的机器学习工具。