多旋翼飞行器坐标系与姿态表示：从欧拉角到四元数

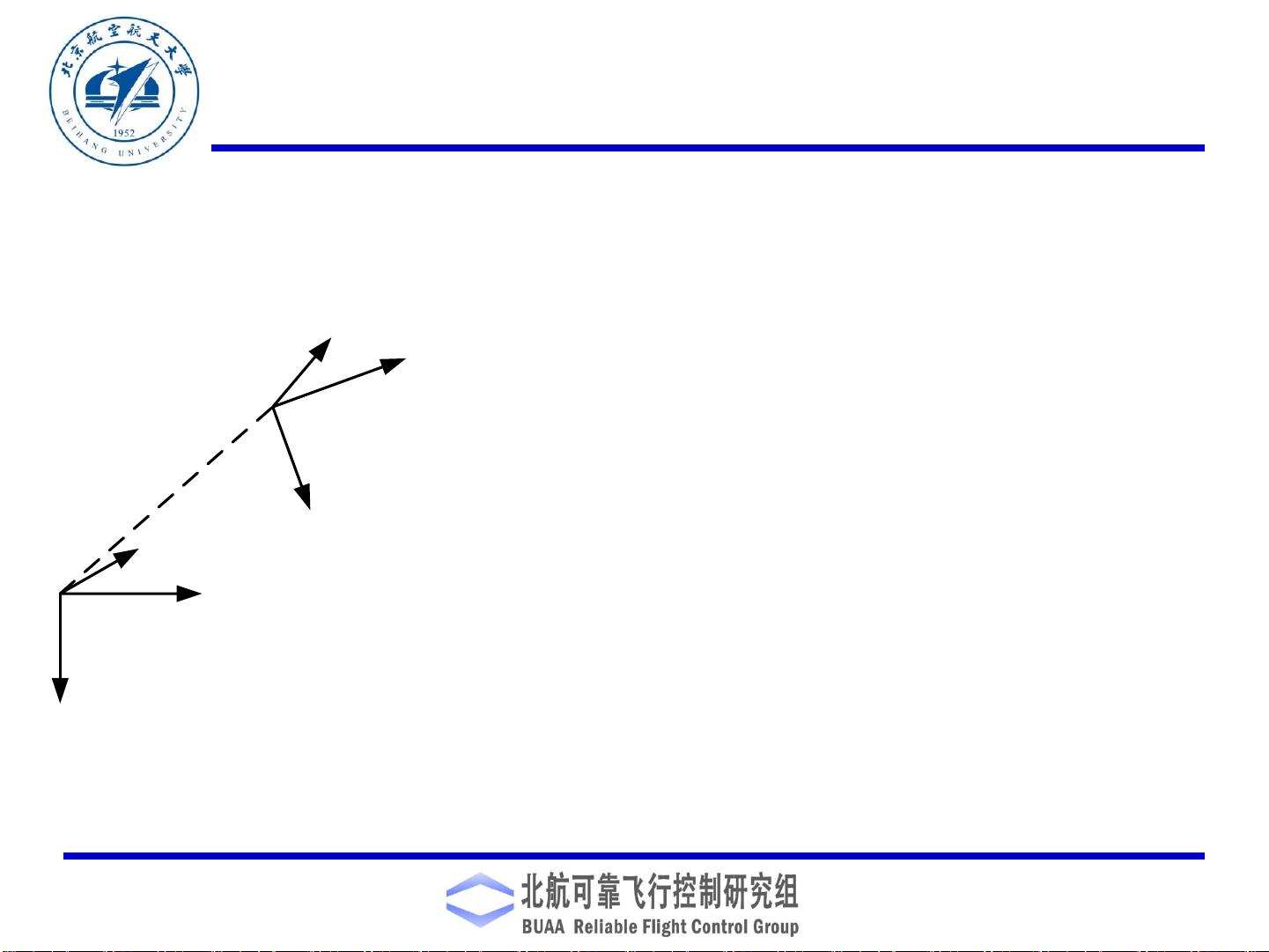
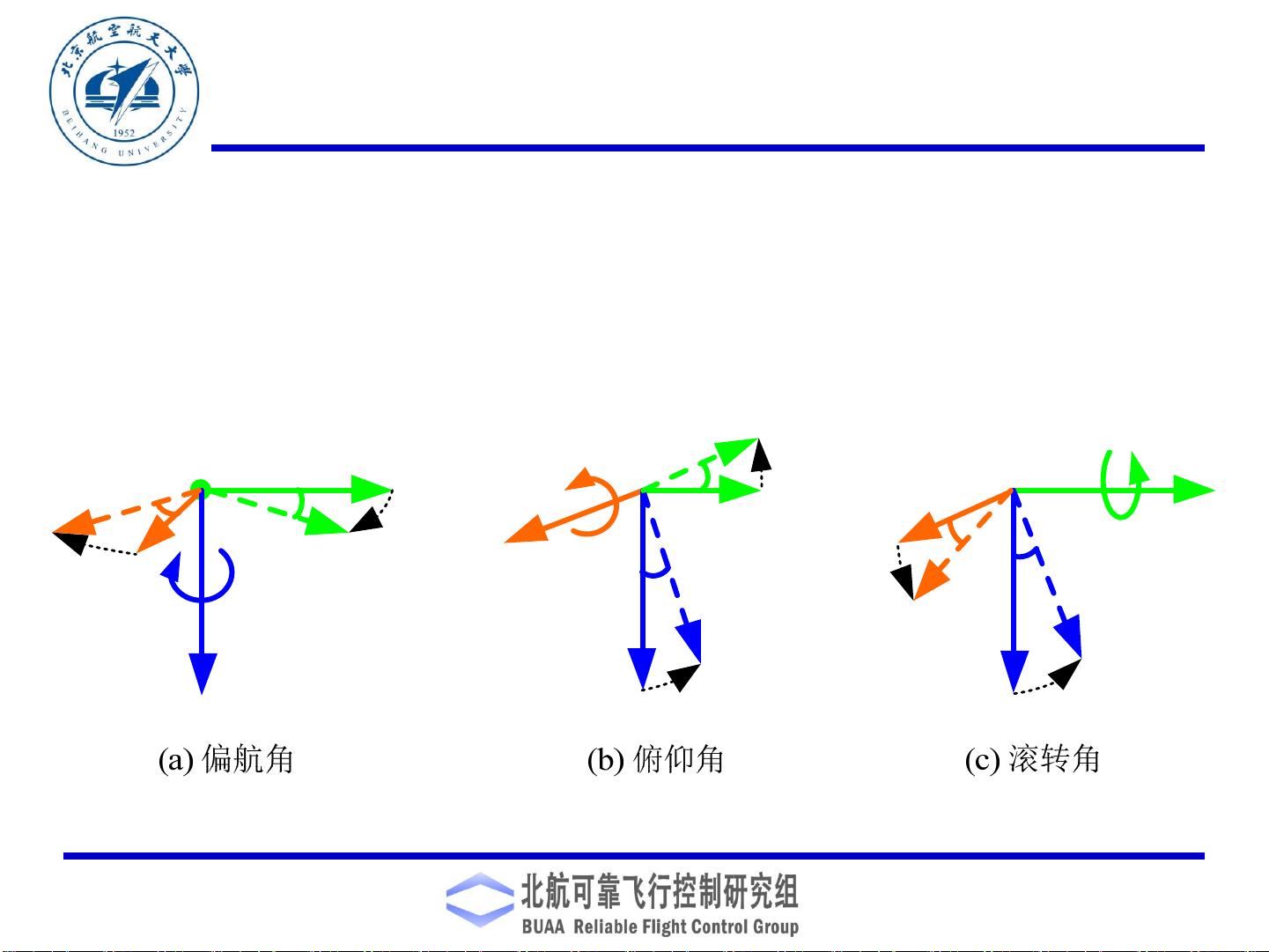
"四元数计算，坐标系和姿态表示的讲解，包括地球固联坐标系与机体坐标系" 在多旋翼飞行器的设计与控制中，理解坐标系和姿态表示是至关重要的。本讲主要涵盖了四种关键概念：坐标系、欧拉角、旋转矩阵和四元数。 首先，坐标系的定义是研究飞行器运动的基础。通常使用两种坐标系，即地球固联坐标系和机体坐标系。地球固联坐标系(e)用于描述飞行器相对于地面的位置和运动，它的原点可以设定在起飞位置或地心，其中x轴指向某一固定方向，y轴通过右手定则确定，而z轴垂直于地面向下。而机体坐标系(b)则是与飞行器固连的，原点位于飞行器重心，x轴指向机头方向，y轴在飞机对称平面内且垂直于x轴，z轴同样通过右手定则确定。 接下来，欧拉角是一种常用的姿态表示方法，它通过三个角度来描述物体相对于参考坐标系的旋转。常见的欧拉角有多种组合，如俯仰(pitch)、翻滚(roll)和偏航(yaw)，分别对应于绕z、x和y轴的旋转。欧拉角的缺点在于存在所谓的万向节死锁(gimbal lock)问题，当两个连续的旋转轴重合时，会导致姿态描述不完整。 旋转矩阵是另一种描述三维空间旋转的方法，它是一个3x3的正交矩阵，表示一个从原坐标系到新坐标系的线性变换。每个旋转矩阵对应一个特定的旋转角度和轴，可以将欧拉角转换为旋转矩阵，反之亦然。旋转矩阵满足乘法性质，可以表示连续的旋转。 四元数是一种更有效的表示三维旋转的数学工具，它克服了欧拉角的万向节死锁问题。四元数由一个实部和三个虚部组成，形式为(q0, q1, q2, q3)，其中q0是实部，q1, q2, q3是虚部。四元数乘法规则可以方便地描述和组合旋转，而且四元数的模长始终保持为1，这有助于保持旋转的保距性。将四元数与旋转矩阵相比，四元数在计算上更为高效，特别是在处理大量旋转操作时。 本讲的小结强调了这些概念在多旋翼飞行器控制中的应用。了解和熟练掌握这些坐标变换和姿态表示方法，对于设计飞行控制器、实现精准定位以及执行复杂的飞行任务至关重要。无论是欧拉角、旋转矩阵还是四元数，它们都有各自的优势和适用场景，选择合适的方法取决于具体的应用需求和计算效率。在实际工程中，通常会结合使用这些工具，以实现最优的控制效果。