"高温作业专用服装设计：稳态与非稳态热传递模型及多目标规划"

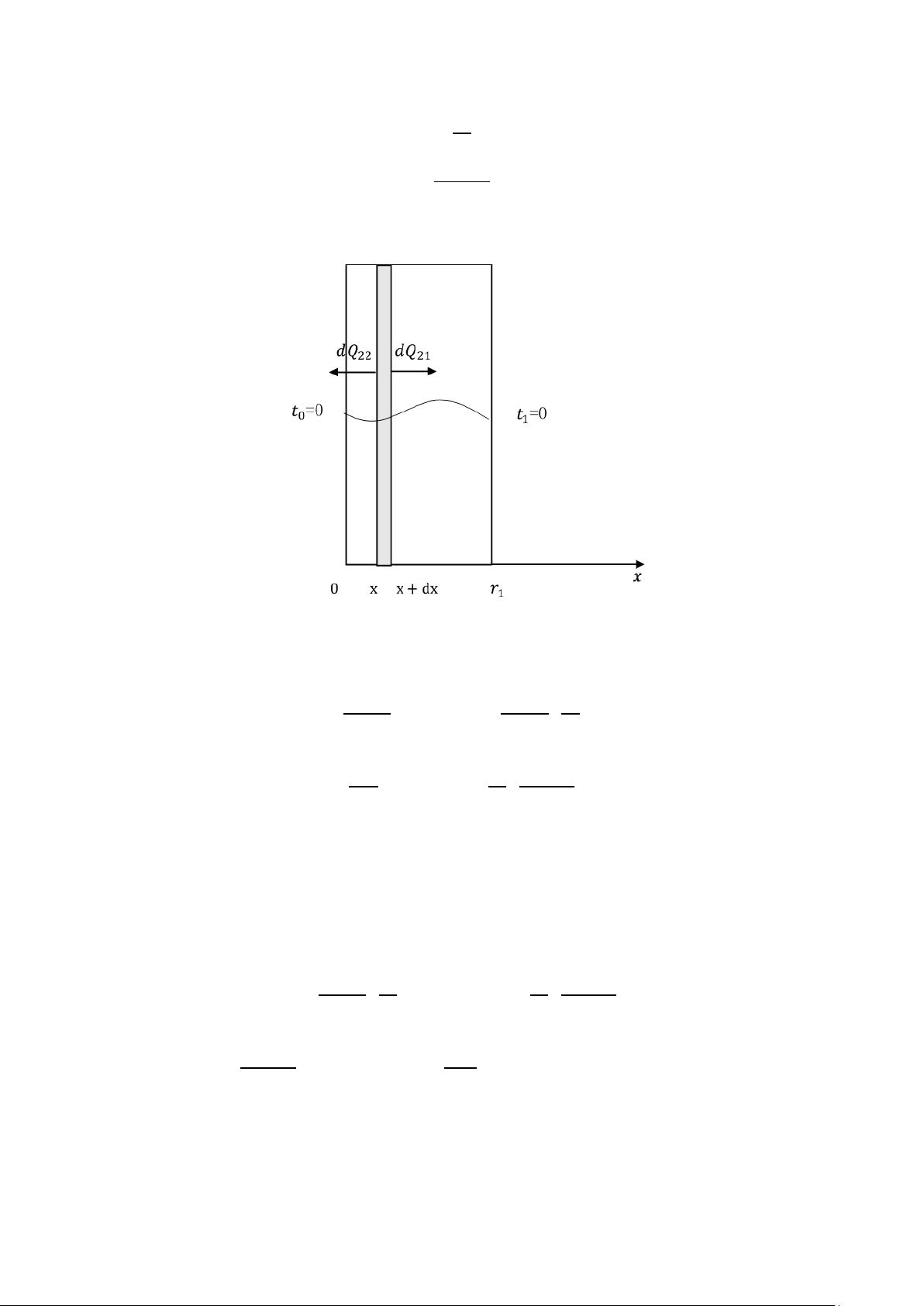
本文针对高温作业专用服装设计问题，分别建立稳态、非稳态热传递微分方程模型，描述了不同时空状态下的温度分布情况；建立基于层次分析法的多目标规划模型，利用蒙特卡罗算法，解决了在特定条件下织物 II 层的最优厚度设计问题；建立了基于双决策变量的多目标规划模型，采用γ −粒子群算法，得到了在特定条件下织物 II 层和空气层IV 层的最优厚度。 针对问题一，对温度变化过程分为非稳态阶段和稳态阶段。对于稳态阶段，首先，建立热阻串联模型，确定三层织物边界温度。接着，建立稳态热传递微分方程模型，得出随着距离的增加，温度随位置变化的函数。对于非稳态阶段，增加时间变量，利用傅立叶定律，建立非稳态热传递微分方程模型，利用基于向后差分的微分方程数值解法，通过离散时空、微分方程、边界条件，得出微分方程数值解格式，以稳态各位置温度为初值向后差分，求解出非稳态温度随时间和位置的分布情况。模型求解结果为在织物的不同层面，温度变化满足不同的函数关系式。彼此变化快慢不一但趋势一致，都呈先快后慢最终趋于稳定的形式，得到隔温服的时空分布矩阵。对模型进行有效性检验显示：模型求解温度和附件中的实验值基本吻合，说明该模型可以较为准确地描述高温作业环境中服装的温度分布情况。 在解决织物 II 层的最优厚度设计问题时，基于层次分析法的多目标规划模型为研究提供了有力的工具。通过蒙特卡罗算法的运用，成功地得到了在特定条件下织物 II 层的最优厚度设计，为高温作业服装的优化设计提供了理论基础和实际指导。而基于双决策变量的多目标规划模型，在采用γ −粒子群算法的情况下，得到了在特定条件下织物 II 层和空气层IV 层的最优厚度，为高温作业服装的设计提供了更加全面和具体的优化方案。这些研究成果不仅提高了高温作业服装的隔热性能，也为高温环境下工作者的健康和舒适提供了保障。 综上所述，本文通过建立了稳态、非稳态热传递微分方程模型，运用层次分析法和双决策变量的多目标规划模型，以及蒙特卡罗算法和γ −粒子群算法等多种数学方法，成功地分析并解决了高温作业专用服装设计问题。通过对温度分布情况的描述和优化设计方案的提出，为高温作业环境下服装设计提供了理论基础和实际指导，有利于提高工作者的工作舒适度和健康保障。未来的研究可以在本文的基础上进一步探讨高温作业服装设计中的其他关键问题，为高温环境下的劳动保护工作提供更多有益的帮助。