上市公司财务指标与盈利预测的线性回归分析

"该资源是一个关于应用商务统计中线性回归分析的 PowerPoint 演示文稿，主要探讨了如何利用线性回归模型预测上市公司的净资产收益率（ROE）。" 在商务统计和金融分析中，线性回归是一种常用的方法，用于研究两个或多个变量之间的关系。在这个案例中，目标是预测中国上市公司下一年的净资产收益率（ROE），基于当年的财务指标。所选取的样本来自深圳和上海股市2002年和2003年的500家上市公司，共计1000个观测值。 案例的目标是建立一个线性回归模型，用以预测ROE，其中自变量包括但不限于以下几点： 1. 当年的净资产收益率（ROE）：可能作为滞后变量，反映公司过去的表现。 2. 资产周转率：衡量公司运用资产产生销售收入的效率。 3. 负债资本比率：评估公司的负债水平与总资产的比例，揭示其财务风险。 4. 价格-账面比率（P/B比率）：反映市场对公司未来盈利能力的预期。 5. 应收账款/主营业务收入：衡量公司收款效率及收入的质量。 6. 主营业务利润/主营业务收入（利润率）：衡量公司的盈利能力。 7. WTH：主营业务增长率：反映公司业务增长的速度。 8. 存货/资产总计：评估公司库存管理效率。 9. （对数）资产总计：考虑公司的规模效应。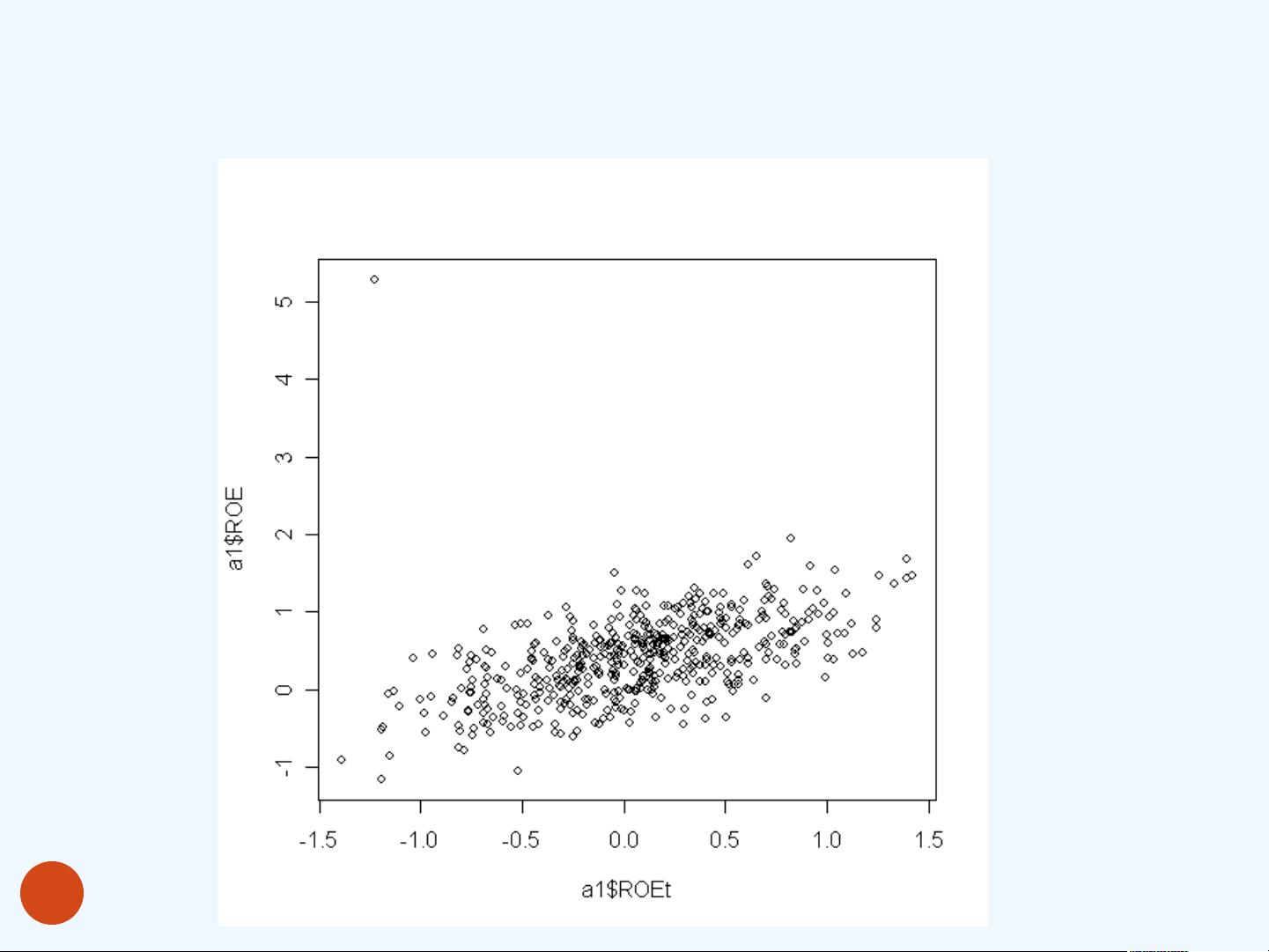 为了分析这些变量与ROE的关系，首先进行了描述性统计分析，这包括读取数据、计算概括性度量（如均值、标准差、最小值、最大值等）以及探索变量间的关系。在SPSS或R环境中，可以执行相应的命令来完成这些任务，例如在R中，可以使用`summary()`函数查看数据概况，`cor()`函数计算变量间的相关性，以及`plot()`函数创建散点图。 接下来，建立了线性回归模型，该模型通常形式为： \[ ROE_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + ... + \beta_p X_{pi} + \epsilon_i \] 其中，\( ROE_i \) 是第i个样本的ROE，\( X_{1i}, X_{2i}, ..., X_{pi} \) 是对应的自变量，\( \beta_0 \) 是截距项，\( \beta_1, \beta_2, ..., \beta_p \) 是自变量的系数，而\( \epsilon_i \) 是误差项。线性回归模型的假设包括： - 独立性假设：误差项之间相互独立。 - 方差齐性假设：所有误差项的方差是相等的。 - 正态性假设：误差项服从正态分布。 参数估计通常采用最小二乘法，这涉及到找到一组系数\( \beta_0, \beta_1, ..., \beta_p \)，使得预测值与实际值之间的平方和最小。在统计软件中，如SPSS或R，可以轻松计算这些估计量。 通过线性回归模型，可以识别哪些自变量在预测ROE时最有效，以及它们的重要性。此外，模型的预测性能可以通过各种统计指标（如R²、调整R²、残差分析等）进行评估。如果模型满足上述假设并且具有良好的预测能力，那么可以利用它来为投资者提供决策支持，帮助他们预测上市公司的未来盈利能力。