信息理论基础:四进制、八进制与二进制信息量比较
需积分: 28 32 浏览量
更新于2024-07-26
1
收藏 1.65MB DOC 举报
"这是关于《信息理论基础》课程的习题解答,主要涵盖了信息量、熵、自信息等相关概念。"
信息理论是通信工程、计算机科学和统计学等领域的重要基础,由克劳德·香农在20世纪40年代创立。它主要研究如何有效地传输和存储信息,并对信息的度量、压缩、编码等问题提供了理论框架。
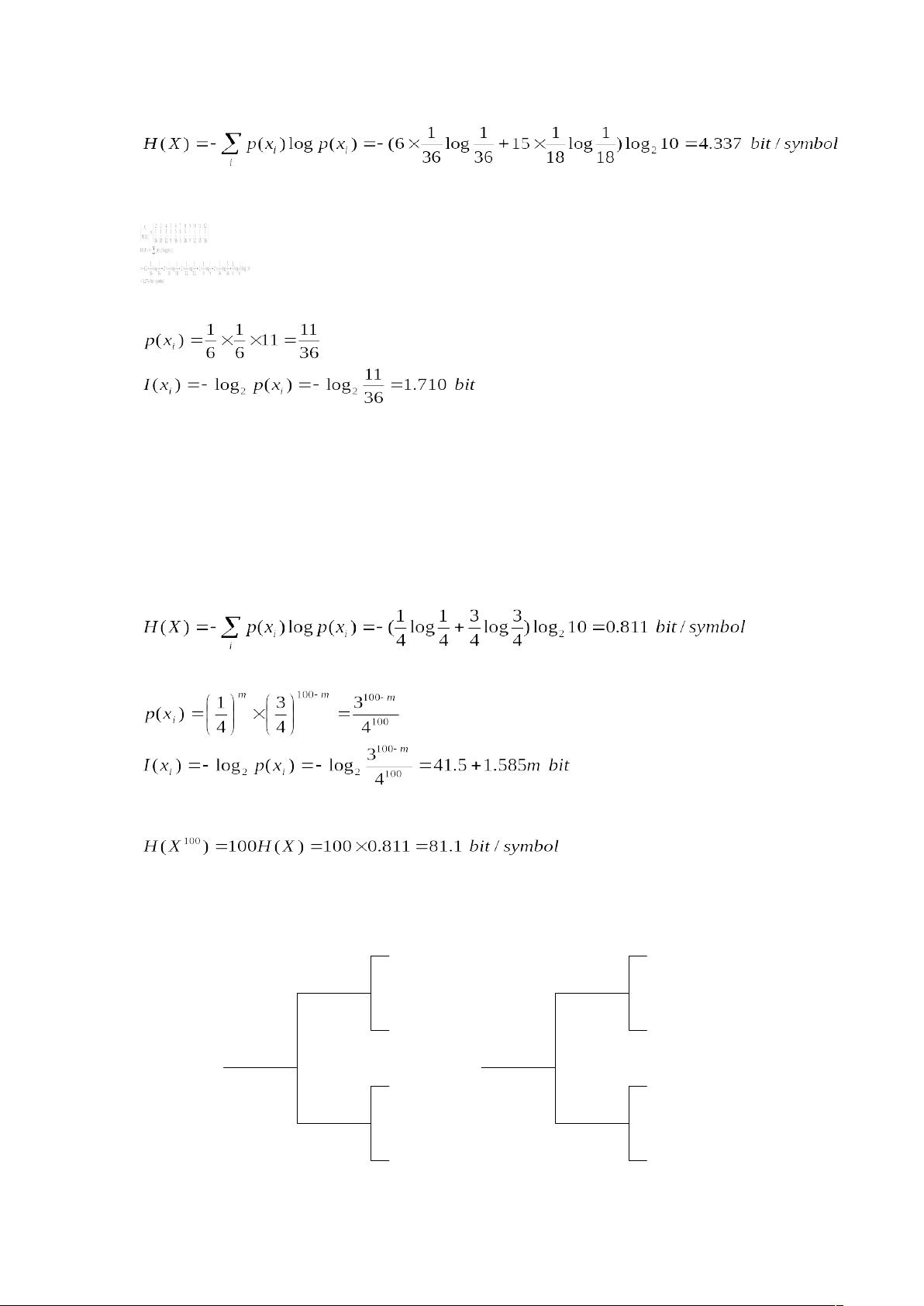
1. 信息量的计算:
- 信息量是衡量一个事件发生所带来的新信息的多少,通常用比特(bit)作为单位。一个事件的信息量可以用它的概率的负对数来表示,即`I(x) = -log2(P(x))`。
- 在问题2.1中,通过计算不同进制脉冲表示的消息数量,我们可以得出四进制和八进制脉冲的信息量分别是二进制脉冲的2倍和3倍。
2. 条件概率与联合概率:
- 条件概率`P(A|B)`表示在事件B发生的条件下,事件A发生的概率。在问题2.2中,我们利用了这个概念来计算得知“身高160厘米以上的某女孩是大学生”这一消息的信息量。首先,分别计算女大学生和所有女孩中身高超过160cm的比例,然后用贝叶斯公式计算条件概率。
3. 熵(Entropy):
- 熵是衡量一个随机变量不确定性或信息量的期望值,对于离散随机变量`X`,熵定义为`H(X) = Σ P(x_i) * log2(1/P(x_i))`,其中`x_i`是随机变量的所有可能取值。
- 在问题2.1中,我们计算了不同进制脉冲的平均信息量,即熵。
4. 自信息(Self-Information):
- 自信息是一个特定事件发生时的信息量,它衡量了该事件发生所带来的意外程度。在问题2.4中,计算了给定消息的自信息和平均信息量。自信息是单个符号的信息量,而平均信息量则是整个消息中所有符号信息量的平均值。
5. 组合概率和计数:
- 在问题2.3中,我们考虑了洗乱的扑克牌排列的问题。第一部分计算了任一特定排列的信息量,使用了排列的总数52!。第二部分涉及抽屉原理,计算了抽取13张不同点数牌的概率。
6. 无记忆信源:
- 无记忆信源意味着当前符号的出现不依赖于之前符号的出现。在问题2.4中,给出了一个离散无记忆信源的例子,通过统计各符号出现的频率来计算消息的自信息量和平均信息量。
信息理论不仅在通信系统的设计中起到关键作用,还广泛应用于数据压缩、密码学、机器学习等多个领域。理解这些基本概念有助于深入探讨和应用信息理论的各种原理。
点击了解资源详情
点击了解资源详情
213 浏览量
692 浏览量
236 浏览量
585 浏览量
211 浏览量
111 浏览量
qwerer4334
- 粉丝: 0
- 资源: 1
最新资源
- arithmetic-progression:js,cpp的算术级数
- html5 canvas+three.js实现的水墨风格云雾变换动画特效源码.zip
- 易语言-PE文件头比较小工具
- Nissan HD Wallpapers JDM Sports Cars Theme-crx插件
- System.Runtime.InteropServices.RuntimeInformation 文件
- firefox-selection-fix:一个脚本,用于禁用Firefox损坏的clickSelectsAll行为
- oc-client-browser:OpenComponents浏览器客户端
- 桔子人才:Desafio Zup桔子人才
- Cross_Slide_Coordinated_Viewing_codeChallenge:该存储库是我对gSoC 2021拟议项目caMicroscope的“交叉滑动协作查看”的代码挑战的提交
- K-Pop-crx插件
- webextensions-history-browser:like像老板一样浏览您的Firefox历史记录
- PowerDesigner导出word模版
- paypal-common-components:PayPal JavaScript SDK的通用组件
- 网页设计2021
- React95:带有Win95 UI的React组件库
- DIYInvestmentPrimer:我们想从我们的投资研究中提供基本和简单的信息