运筹学第一章:线性规划详解
需积分: 12 139 浏览量
更新于2024-07-30
2
收藏 1.19MB PDF 举报
"该资源是天津大学提供的关于运筹学第一章——线性规划的PDF教程,主要内容包括线性规划的模型与图解法、单纯形法、对偶问题与灵敏度分析、运输问题以及线性整数规划。教程中通过实例介绍了如何构建线性规划模型,以解决如何在有限资源下最大化效益的问题。"
线性规划是一种优化技术,常用于决策问题,尤其是在生产管理、经营活动中,旨在合理分配有限的资源以获得最大收益。线性规划问题通常包含以下几个核心组成部分:
1. **决策变量**:线性规划中的关键元素,代表需要决策的未知量,例如在案例中,甲、乙产品的计划产量就是决策变量。
2. **目标函数**:要优化的量,即决策的目标,通常用决策变量的线性组合来表示。在上述例子中,目标函数是总收入,希望最大化。形式上,目标函数为 `Max z = c1x1 + c2x2`,其中 `z` 是目标值,`c1` 和 `c2` 是对应于产品 `x1` 和 `x2` 的单位价格。
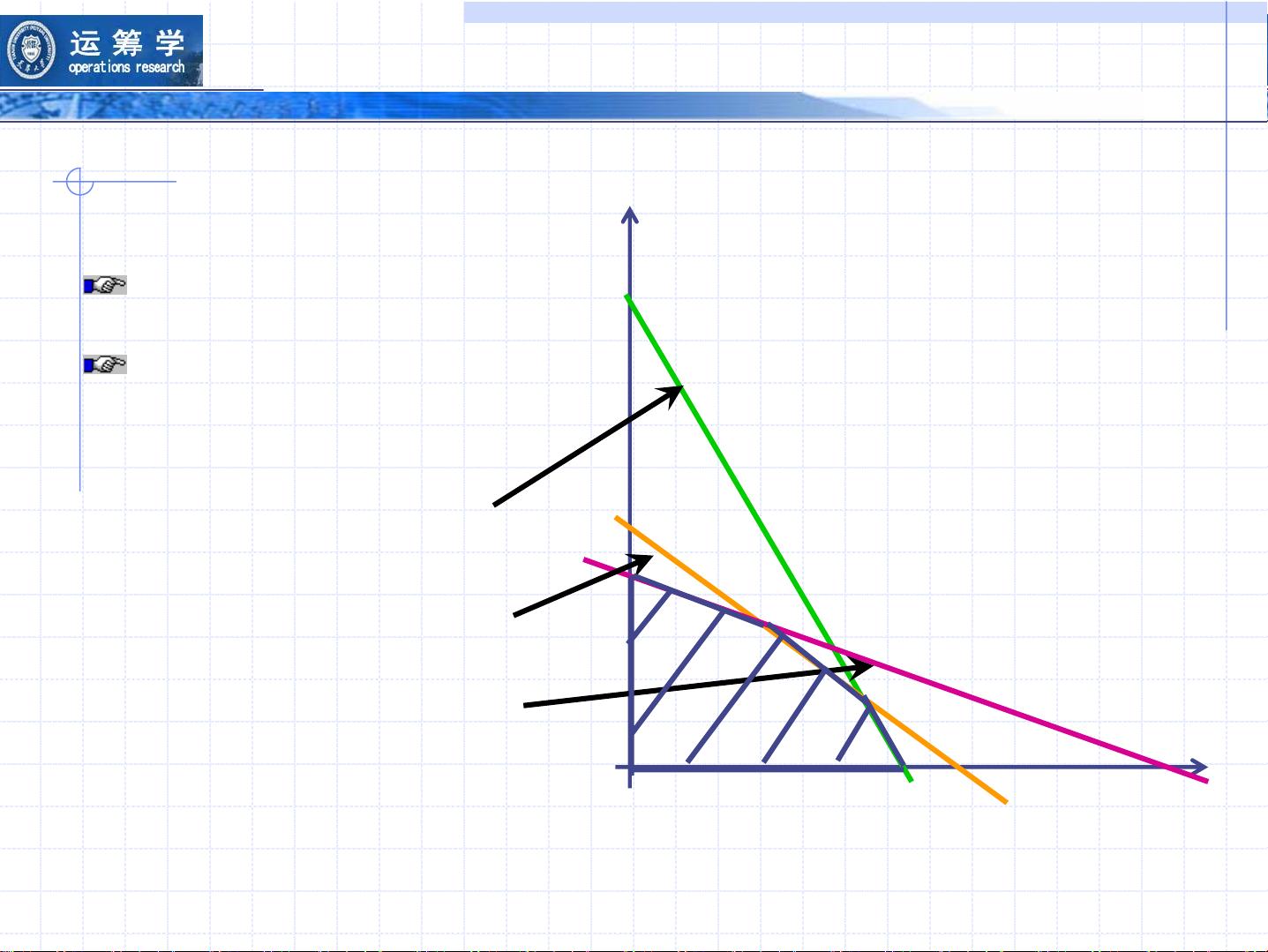
3. **约束条件**:定义了决策变量可以取值的范围,这些条件通常由决策变量的线性等式或不等式构成。在上述例子中,约束条件来自各种资源的限量以及产量非负的限制,如 `x1 ≥ 0, x2 ≥ 0, 94x1 + 45x2 ≤ 300, 10x1 + 5x2 ≤ 200, 3x1 + 4x2 ≤ 360`。
线性规划模型的基本特征是所有的决策变量、目标函数的系数以及约束条件都是线性的。这意味着目标函数和约束条件由一次多项式组成,没有二次或更高次的项。
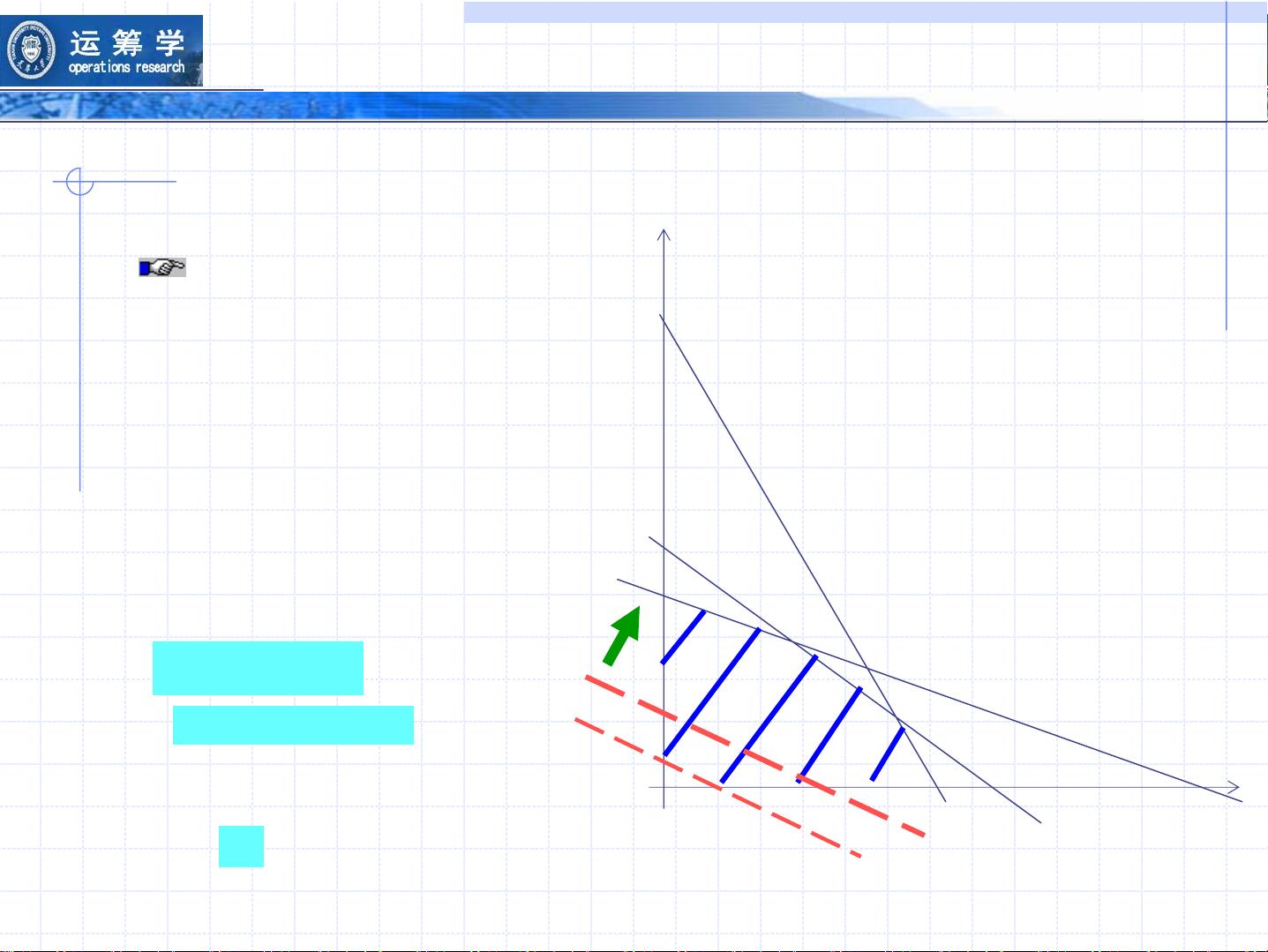
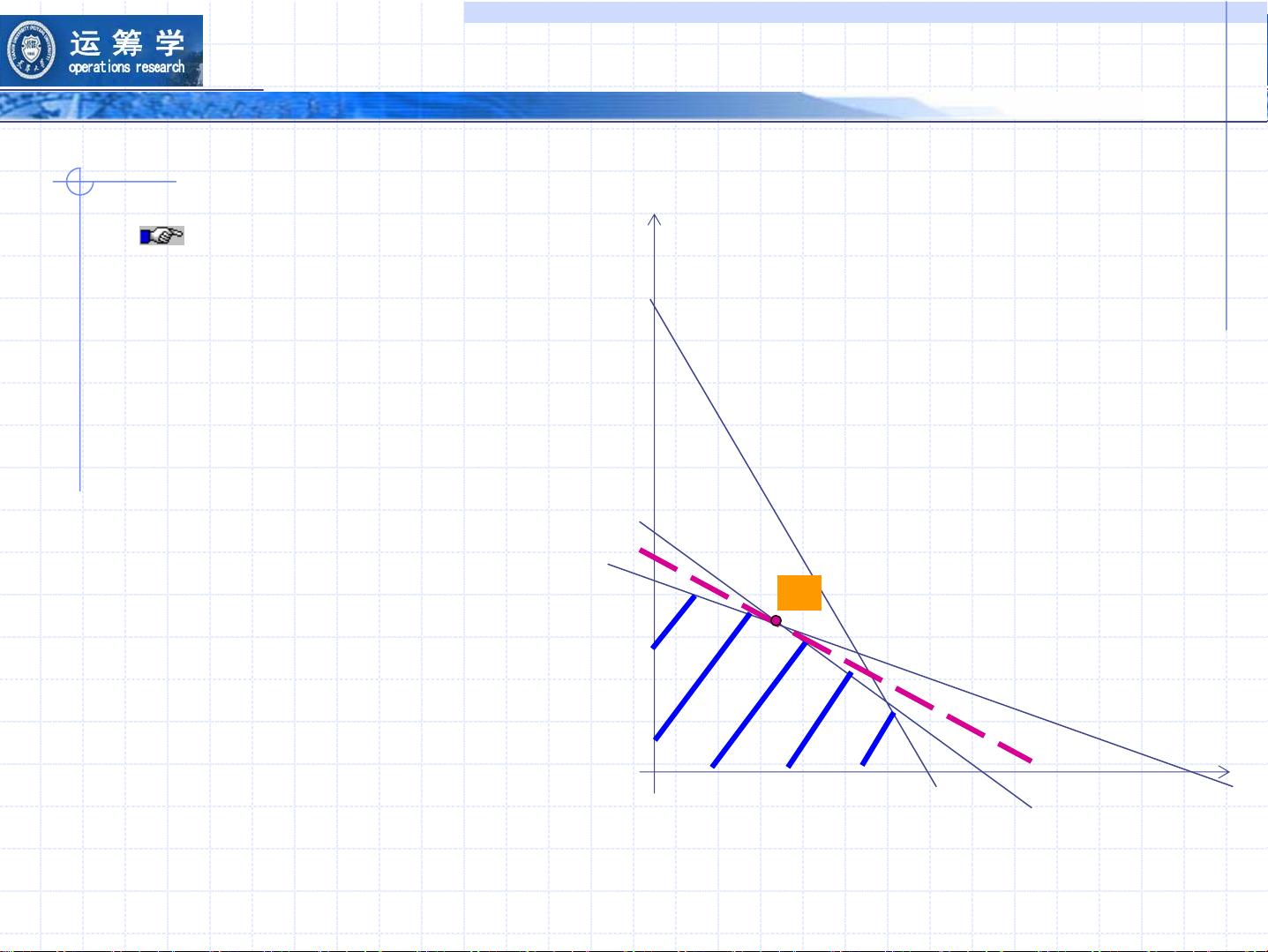
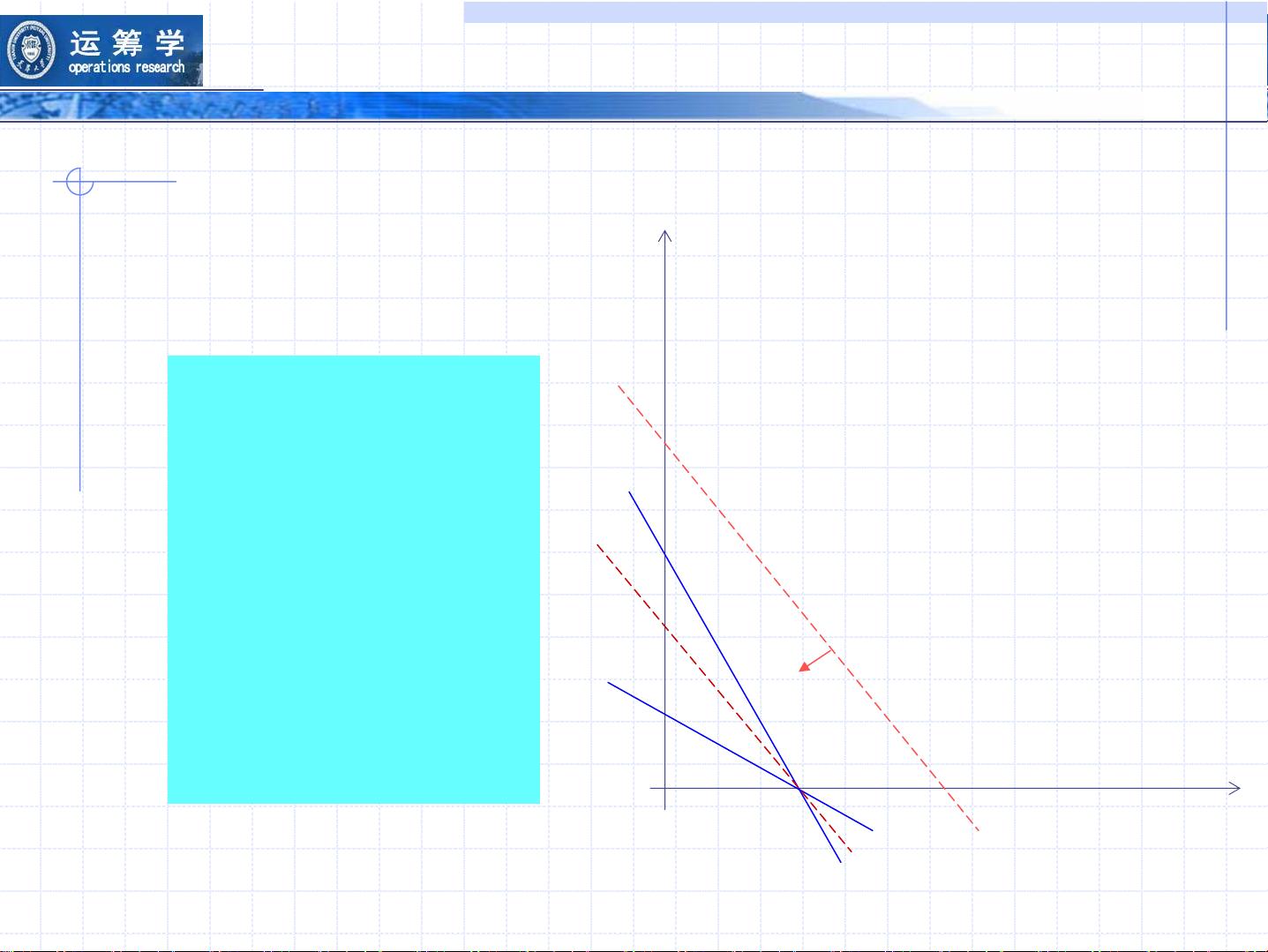
线性规划的解决方案可以通过多种方法找到,其中包括图解法(适用于二维问题)和更通用的单纯形法。单纯形法是一种迭代算法,适用于高维问题,能够找到满足所有约束条件下的目标函数最优解。此外,对偶问题是对原问题的另一种形式,它提供了对原始问题的洞察,并且在灵敏度分析中扮演重要角色,可以帮助分析参数变化对解的影响。
线性规划的应用广泛,例如在运输问题中,它可以帮助确定从产地到销地的最佳运输方案,以最小化运输成本或最大化利润。线性整数规划则进一步扩展了线性规划,允许决策变量取整数值,增加了问题的真实性和复杂性,但同时也引入了新的算法挑战。
线性规划是运筹学的基础,是解决实际生活中众多资源分配问题的有效工具,对于理解和应用现代优化理论至关重要。
2021-10-23 上传
2009-02-27 上传
279 浏览量
740 浏览量
2010-08-23 上传
2024-07-04 上传
w906062553
- 粉丝: 1
- 资源: 13
最新资源
- EXT开发的一个实用教材
- IBM官方的AIX5.2的图文安装指南
- Shell 設計入門,很详细的教学笔记
- HTML常用特殊字符的编码
- 2008年[下半年]软件设计师[下午B卷].pdf
- Arm Linux开发笔记.pdf
- 2008年[下半年]软件设计师[上午B卷].pdf
- oraclereleasenote(linuxx86)
- install oracle10g on linux
- sap人力资源配置实现
- Web_Service开发指南_2.3.1
- Getting Started with Flex 3 英文原版 Adobe 官方资源
- 人才数据库及网站的设计毕业论文
- 硬件维护试题2007年3月
- CUDA资料的学习,特别初学者
- td de xue xi