Linux入门：文件系统、Shell命令与挂载解析

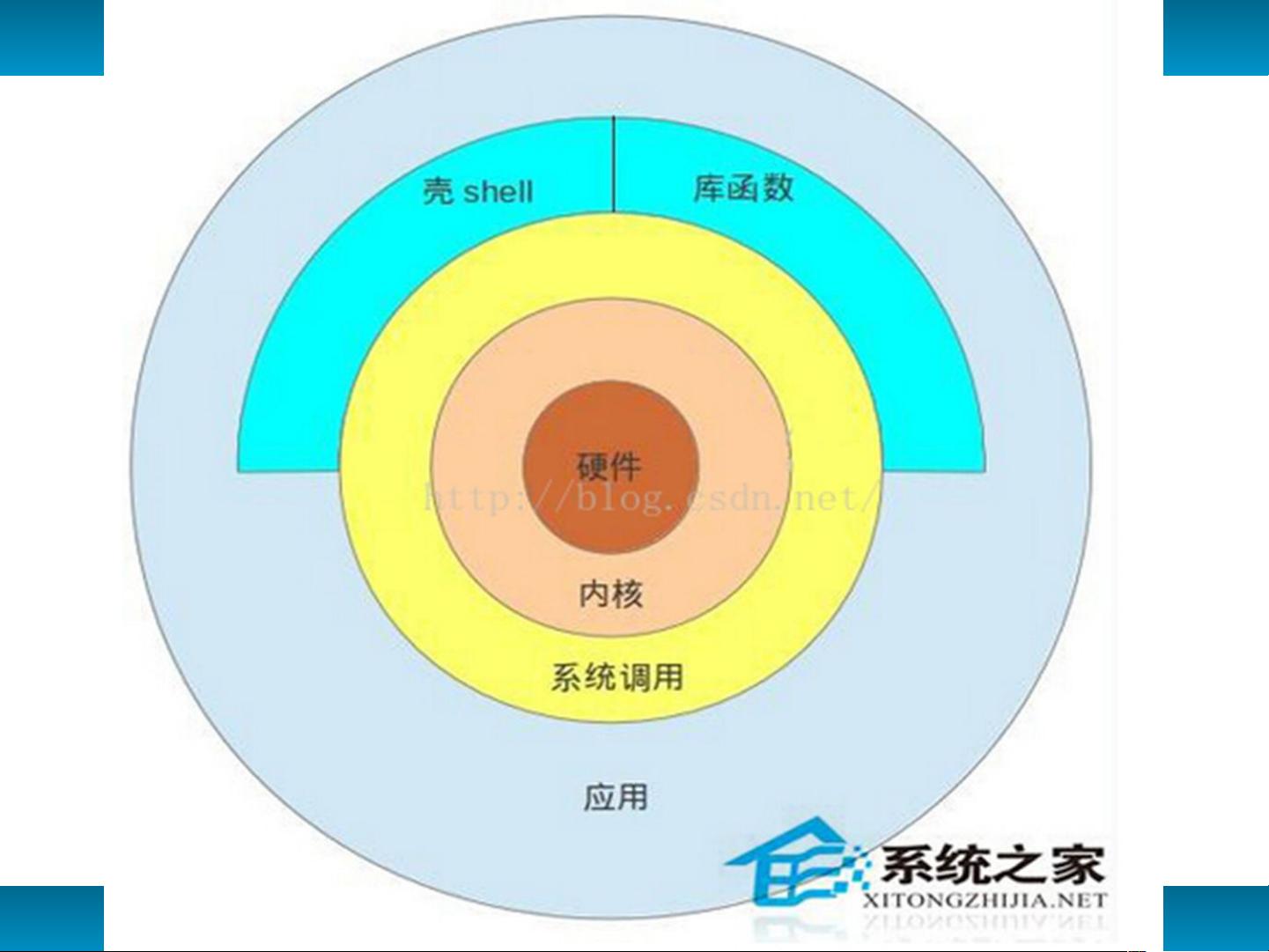
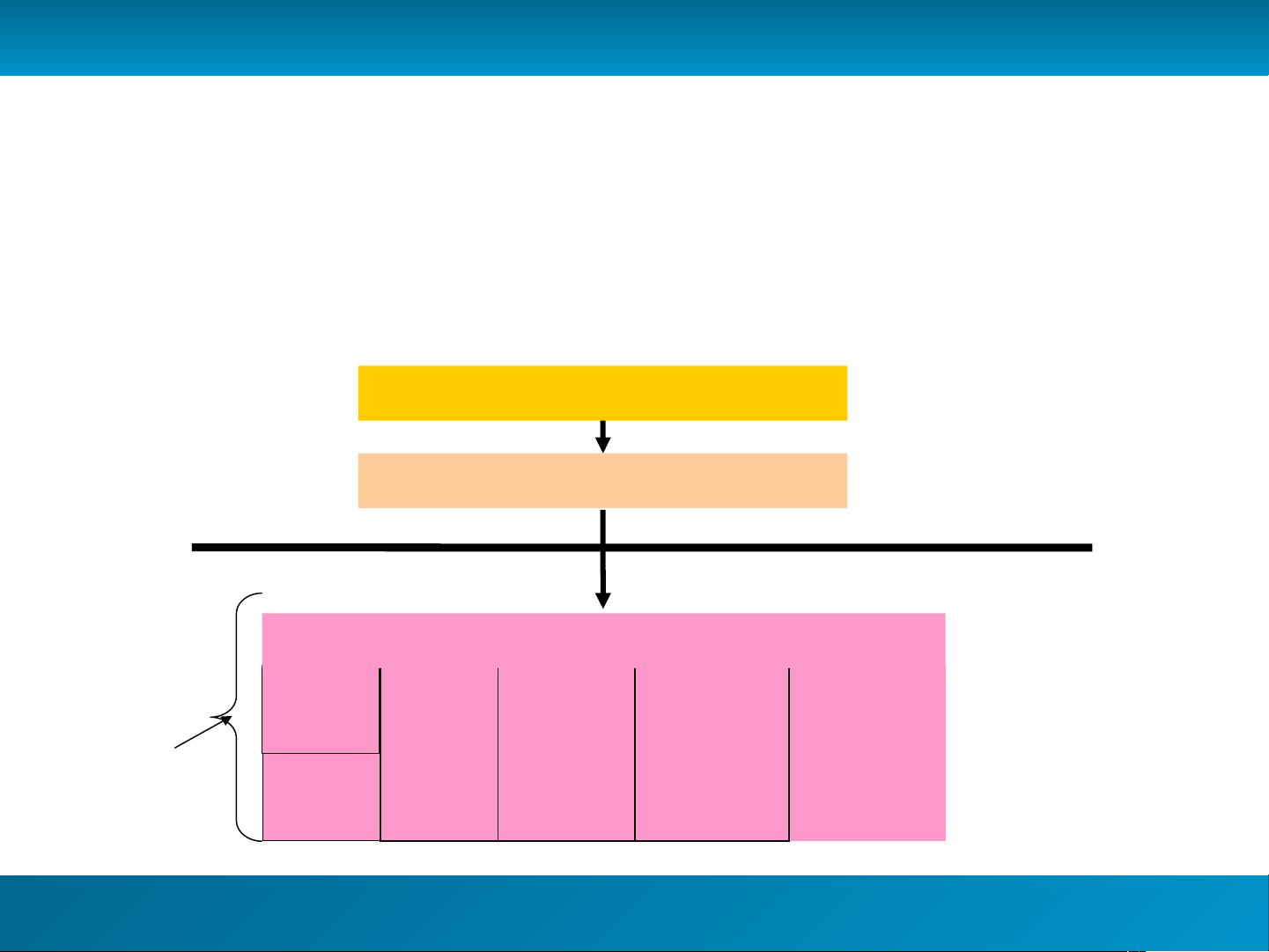
本资源是关于Linux操作基础的讲解，主要涵盖了Linux文件系统、Shell以及常用的命令。适合初学者了解和学习Linux系统的基本操作。 在Linux操作系统中，文件系统是至关重要的组成部分，它负责管理存储设备上的文件组织、分配、保护和检索。Linux常用文件系统类型包括Ext2、Ext3和Ext4，而Windows则有FAT12、FAT16、FAT32以及NTFS。Linux文件系统采用一种称为目录树的逻辑结构，其中每个目录和文件都有特定的权限。 在Linux文件系统中，硬链接和软链接是两个特殊概念。硬链接是指在不同的目录下创建一个新的文件，该文件直接指向原始文件的inode（文件元数据的存储节点），这样可以节省硬盘空间，因为多个硬链接共享同一个inode，无需复制文件内容。而软链接，也称为符号链接，是创建一个指向源文件路径的文本文件，当源文件被删除时，软链接将变成无效。 挂载是Linux系统中另一个关键的概念，它是将分区与目录树中的特定目录关联的过程。根目录“/”是整个系统的基础，所有其他目录都从这里扩展。Linux系统启动时，至少有一个分区（根分区）挂载到“/”，其他分区可以挂载到“/”下的特定子目录，如“/mnt”或“/media”。常见的分区还包括swap分区（用于虚拟内存）、home分区（用户个人文件）、bin（二进制执行文件）和usr（用户软件）等。 此外，Linux操作基础还包括Shell及其常用命令的学习。Shell是Linux的命令行界面，用户可以通过它输入命令来与系统交互。一些基础命令如ls（列出目录内容）、cd（改变目录）、pwd（显示当前工作目录）、cp（复制文件）、mv（移动或重命名文件）和rm（删除文件）等，是Linux用户日常操作中不可或缺的工具。 这份资源将帮助学习者掌握Linux文件系统的基本概念、硬链接和软链接的区别，以及如何理解和操作挂载点。同时，还会引导他们熟悉常用的Shell命令，为更深入的Linux系统操作打下坚实的基础。