能源采集推动无线通信最新进展综述

需积分: 1 9 浏览量更新于2024-07-20 收藏 2.23MB PDF 举报

近年来，随着无线通信技术的不断发展和环保意识的提升，能源采集（Energy Harvesting）在传感器网络中的应用逐渐成为研究热点。本文综述了这一领域的最新进展，由S.Ulukus、A.Yener、E.Erkip、O.Simeone、M.Zorzi、P.Grover和K.Huang等学者共同编撰，关注的是能量自给自足的无线网络设计与优化。文章首先阐述了无线网络中引入能量采集节点的重要性，这使得设备不再完全依赖外部电源，从而实现了更长时间的运行和更广泛的环境适应性。作者从信息理论的角度探讨了能量采集网络的性能极限，包括传输效率、数据速率和可靠性，这些都是衡量无线通信质量的关键指标。在技术层面，文中深入研究了能量传输策略，特别是能源合作（Energy Cooperation）的概念，即多个节点之间共享和交换能量，以实现整体能源的协同利用。同时，文章还关注了同时无线信息和能量（SWIPT，Simultaneous Wireless Information and Power Transfer）传输技术，这是一种创新方法，允许在同一个信号传输过程中同时传输数据和提供能量，极大地提高了资源利用率。文章涵盖了不同规模的网络模型，从微型设备到大规模分布式系统，都对能量消耗模型进行了详尽分析，这对于优化网络架构和设计具有实际指导意义。此外，文章还讨论了节点层面的能量管理策略，如动态调整工作模式、优化能效算法等，以确保在有限的能源条件下实现高效通信。索引术语中提到了几个核心概念，包括能源采集通信、能源合作以及SWIPT，这些都是推动当前和未来无线网络发展的重要驱动力。通过这些研究，科学家们正在努力突破技术瓶颈，为构建更加绿色、可持续的无线通信网络奠定基础。这篇综述文章提供了关于能量采集无线通信领域的广泛视角，不仅总结了已有的研究成果，还对未来的研究方向和挑战进行了展望，对于理解和应用能源采集技术的工程师和研究人员来说是一份极具价值的参考资料。

curve

tightest

curve

(

− E

max

)

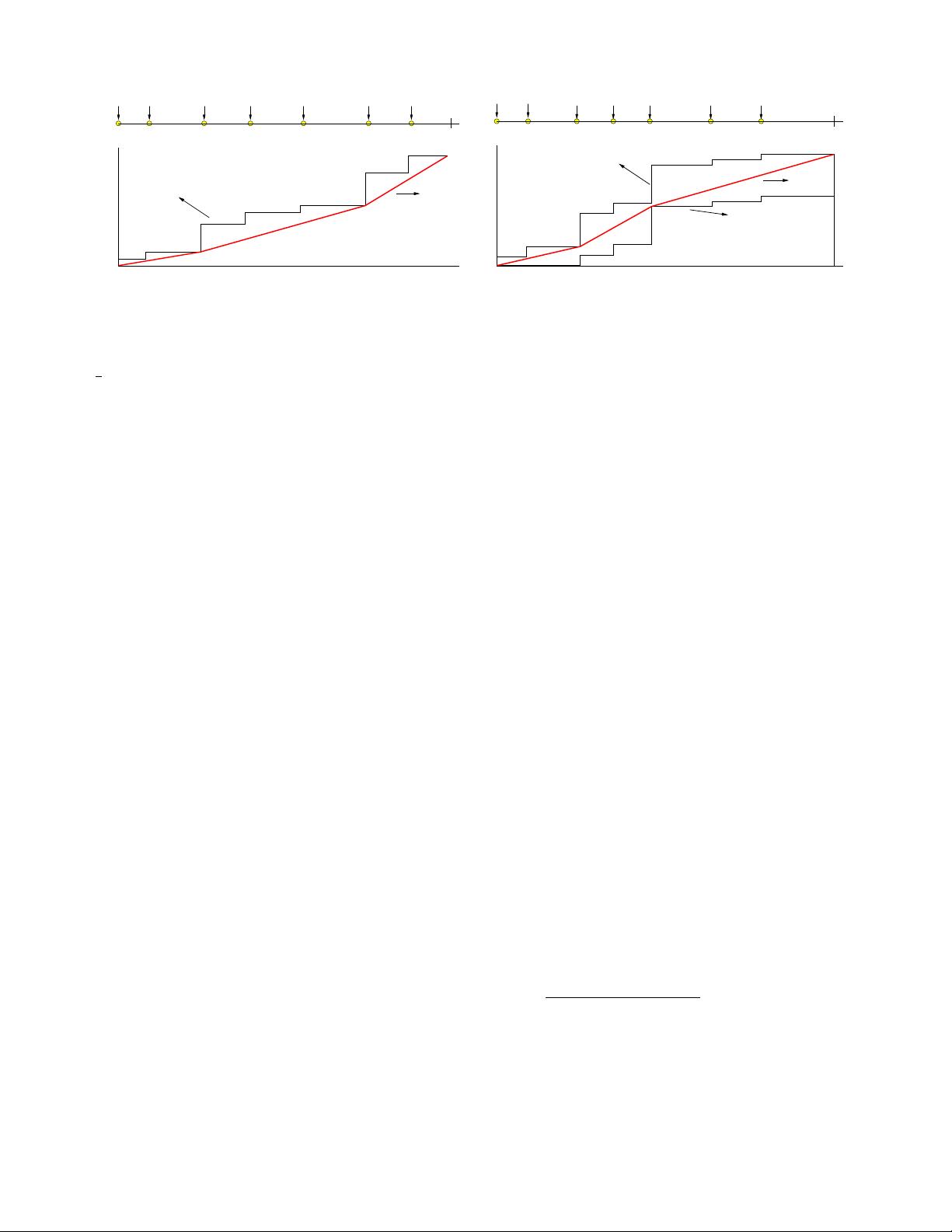
(a) (b)

Fig. 4. The optimal policy is the tightest string that connects the two ends. (a) E

max

= ∞. (b) Finite E

max

we send a signal with power P in an epoch of duration

log (1 + hP ) bits of data are served out from the data

backlog with the cost of `P units of energy depletion from

the energy queue. With this model in mind, we solve for the

optimum power control policy P (t) in time as a function of the

energy arrival proﬁle, the data backlog proﬁle and the channel

fading proﬁle, in order to minimize the time by which all

of the packets are successfully transmitted. Minimizing the

transmission completion time for a given number of bits is

equivalent to maximizing the number of bits transmitted in

a given duration. Therefore, in the following, we consider

maximizing the number of bits delivered by a deadline T .

The optimization problem is subject to the energy causality

constraint on the harvested energy, and the ﬁnite-storage

constraint on the rechargeable battery. In particular, the energy

causality constraint requires that the energy that has not arrived

yet (has not been harvested yet) cannot be used. The ﬁnite-

storage constraint, on the other hand, requires that no energy

is wasted because of battery being full at the time of energy

arrivals; we also call this constraint the no-energy-overﬂow

constraint. Assume that energies of {E

, E

, . . . , E

N−1

} are

harvested, and epoch lengths are {`

, . . . , `

N−1

}. Due to the

concavity of the rate-power relationship, power must be kept

constant between energy harvests [12]. This reduces the power

control policy of P (t) to a sequence of constant powers

, . . . , p

}. The energy causality constraints become [12]

i=1

≤

k−1

i=0

, k = 1, . . . , N (5)

and the no-energy-overﬂow constraints become [13]

i=0

−

i=1

≤ E

max

, k = 1, . . . , N − 1 (6)

We illustrate these two constraints on the energy consump-

tion policy in Fig. 3(b). The upper staircase is the cumulative

energy arrival proﬁle which provides the energy causality

upper bound, and the lower staircase is the no-energy-overﬂow

curve which provides a lower bound. Any feasible energy

consumption curve must lie in between. We note that the

energy causality constraint forces the energy consumption to

slow down not to exceed the harvested amount, while the no-

energy-overﬂow constraint forces energy consumption to speed

up to open up space in the battery for new energy arrivals.

Although the optimization is over all monotonically non-

decreasing time functions for the energy consumption curve,

by the concavity of the objective function, the optimal policy

must remain constant in between energy harvests; therefore,

the dimension of the optimization problem is reduced to the

ﬁnite number of epochs in an interval. Geometrically, this

means that the feasible energy consumption proﬁles which

are candidates to be optimum must be piece-wise linear. The

optimal policy is shown to be the tightest string that lies in

the energy feasibility tunnel [12], [13]. This solution aims to

keep longest stretches of constant power periods subject to

energy causality and no-energy-overﬂow constraints, as the

concavity of the power-rate relationship favors constant powers

to the extent possible. An example of the optimum energy

consumption curve is shown in Fig. 4(a) for E

max

= ∞, i.e.,

there is no energy overﬂow concerns, and in Fig. 4(b) for a

ﬁnite E

max

An alternative approach to the feasible tunnel approach is

the directional water-ﬁlling algorithm presented in [14]. The

directional water-ﬁlling algorithm aims to distribute the water

(energy) equally over time, subject to energy causality con-

straints, which introduce the directionality of water (energy)

ﬂow. The directional water-ﬁlling algorithm requires walls at

the points of energy arrival, with right permeable water taps

in each wall which allows water to ﬂow only to the right. This

implements the energy causality constraint, i.e., energy can be

saved and used in the future, but the energy that will arrive

in the future cannot be used before it has arrived. In addition,

these taps allow at most E

max

amount of water to ﬂow to the

right. This implements the ﬁnite-capacity battery constraint by

avoiding overﬂows. These are based on the KKT optimality

conditions found from the corresponding convex optimization

problem [14]

∗



N+1

j=i

−

j=i



− 1, i = 1, . . . , N (7)

where λ

are the Lagrange multiplier that enforce energy

causality and µ

are the Lagrange multipliers that enforce

no-energy-overﬂow conditions. In the implementation of the

directional water-ﬁlling algorithm, ﬁrst, the taps are kept off,

and transfer from one epoch to the other is not allowed. Then,

the taps are turned on one by one, and at most E

max

−E

units

of energy transfer from past to the i+1st epoch is allowed. An

剩余21页未读，继续阅读

聆听万物说

粉丝: 0
资源: 7

能源采集推动无线通信最新进展综述

Review of Scientific Instruments (RSI) 文章模板与提交指南

Gnome Review Orb Of Magic：简化Git代码审查流程

"2018世界液化天然气报告：全球行业现状、贸易数据及国家间互动

A review of recent range image registration methods with accuracy evaluation.pdf

Brief review of recent research on blue phase liquid crystal materials and devices

A Thorough Review on Recent Deep Learning Methodologies for Ima

Matching teaching to learners: A review of a decade of research

A review of recently developed measures of adaptive behavior

A review of data mining techniques

A Review of Biomedical Centrifugal Microfluidic Platforms

最新资源