贝叶斯网络详解:概念与实践入门
需积分: 10 125 浏览量
更新于2024-08-02
收藏 1.03MB PDF 举报
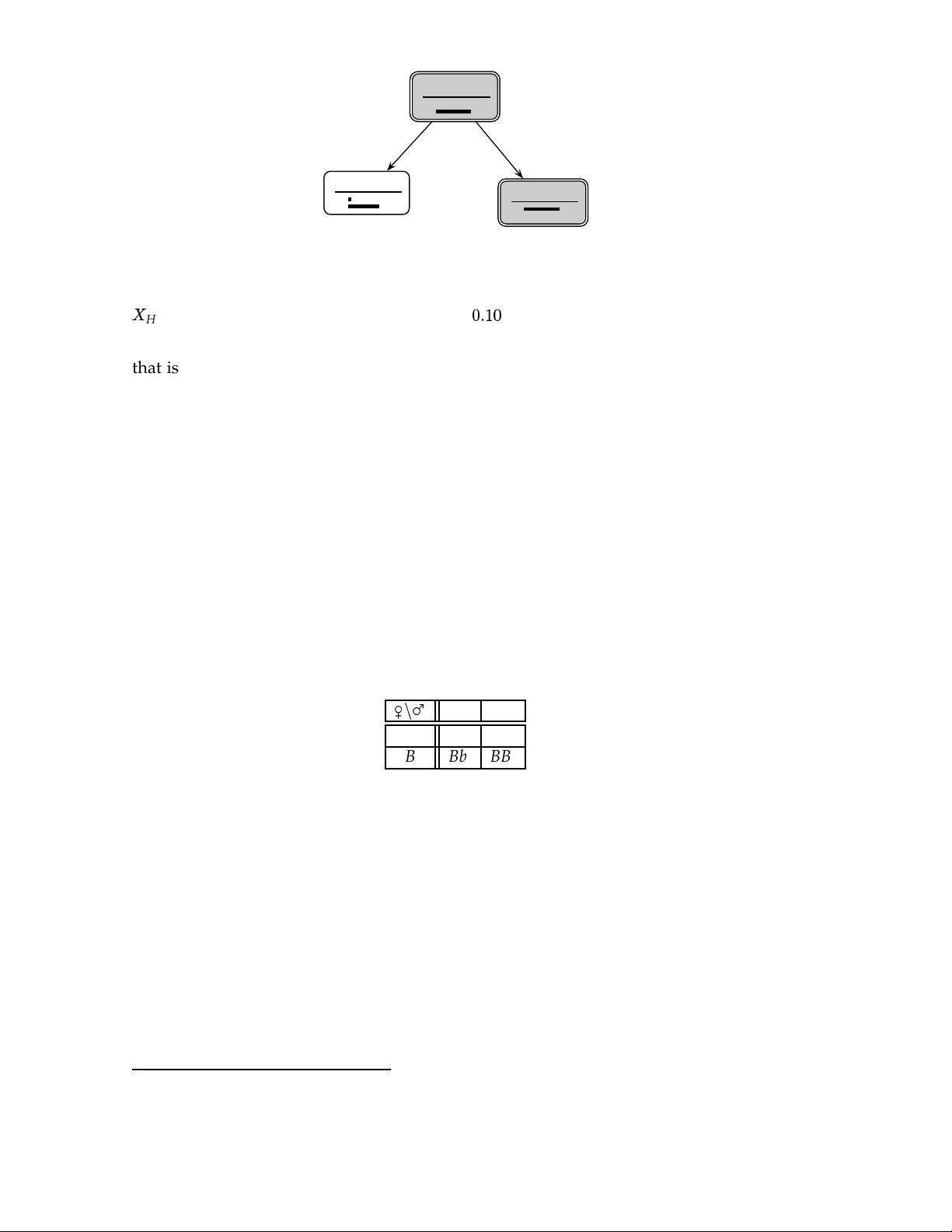
贝叶斯网络(Bayesian Networks)是一种强大的概率图模型,用于表示和推理复杂系统的不确定性。它由节点和边组成,每个节点代表一个随机变量,而边则表示这些变量之间的条件依赖关系。在本篇介绍中,我们首先从概念层面理解这个工具,它是如何通过概率理论来建模现实世界中的事件及其相互影响。
在贝叶斯网络中,每个节点都有一个概率分布,通常是伯努利、二项式、多项式或高斯分布,根据节点变量的类型。节点之间的关系是通过贝叶斯法则来定义的,即给定其他节点的状态,每个节点的概率可以通过条件概率公式计算。这种结构使得网络能够有效地处理缺失数据,并在不确定环境中进行预测和决策。
举例来说,提供的数据展示了不同领域(如电力、电信、航空、银行、股票市场、公用事业和交通)的工作状态(Working, Reduced, NotWorking)与可能的后果(如Up/Down/Crash等)。在这个上下文中,贝叶斯网络可以用来分析故障率、服务稳定性等,通过学习每个领域的先验概率以及故障状态之间的相互影响,我们可以进行故障诊断、风险评估或者预测未来的事件可能性。
网络的实施涉及到编程实现,例如在Python中,我们可以使用专为贝叶斯网络设计的库,如`pomegranate`或`pgmpy`。在实际应用中,我们需要收集并整理相关数据,确定节点和边的结构,然后利用贝叶斯定理更新节点的概率,进行后验推理。此外,贝叶斯网络也常用于机器学习领域中的分类、序列标注、推荐系统等多个任务,其强大的适应性和可扩展性使其在处理复杂的因果关系问题时表现出色。
总结来说,学习贝叶斯网络是一个重要的技能,特别是在数据分析、人工智能和机器学习领域。它提供了一种直观且有效的工具,帮助我们理解和处理不确定性,是理解和应用概率统计知识的重要桥梁。对于希望深入学习这一主题的人来说,强烈推荐这个英文版的入门教程,作者Henrik Bengtsson的讲解将引导你逐步掌握贝叶斯网络的基本原理和实践技巧。
点击了解资源详情
点击了解资源详情
点击了解资源详情
120 浏览量
105 浏览量
221 浏览量
176 浏览量
134 浏览量
2012-03-21 上传
mark_cao1983
- 粉丝: 0
- 资源: 1
最新资源
- salvageo-crx插件
- 空中数控移动
- 易语言专用MP3播放器
- simplelog
- 按键输入与蜂鸣器 - .zip
- libGLESv2_libglesv2_leafga7_sdhyuj_
- 易语言bass可视化效果器
- ArticutAPI:Articut的API中文断词(兼具语意词性标记):「断词」又称「分词」,是中文资讯处理的基础。Articut不用机器学习,不需资料模型,只用现代白话中文语法规则,即能达到SIGHAN 2005 F1-measure 94%以上,召回96%以上的成绩
- local
- Logene归档
- chrome谷歌浏览器驱动(100.0.4896.60)
- sweetheart.py:在Speedlight上构建包括AI在内的全栈Web应用程序
- expansion_game:用 HTML 和 JS 重新制作“生命游戏”
- 标题::beach_with_umbrella:轻松培训和部署seq2seq模型
- react-webpack-starter:使用React,Webpack和Bootstrap的入门
- proxmox-dns