理解支持向量机：SVM的概念与优势解析

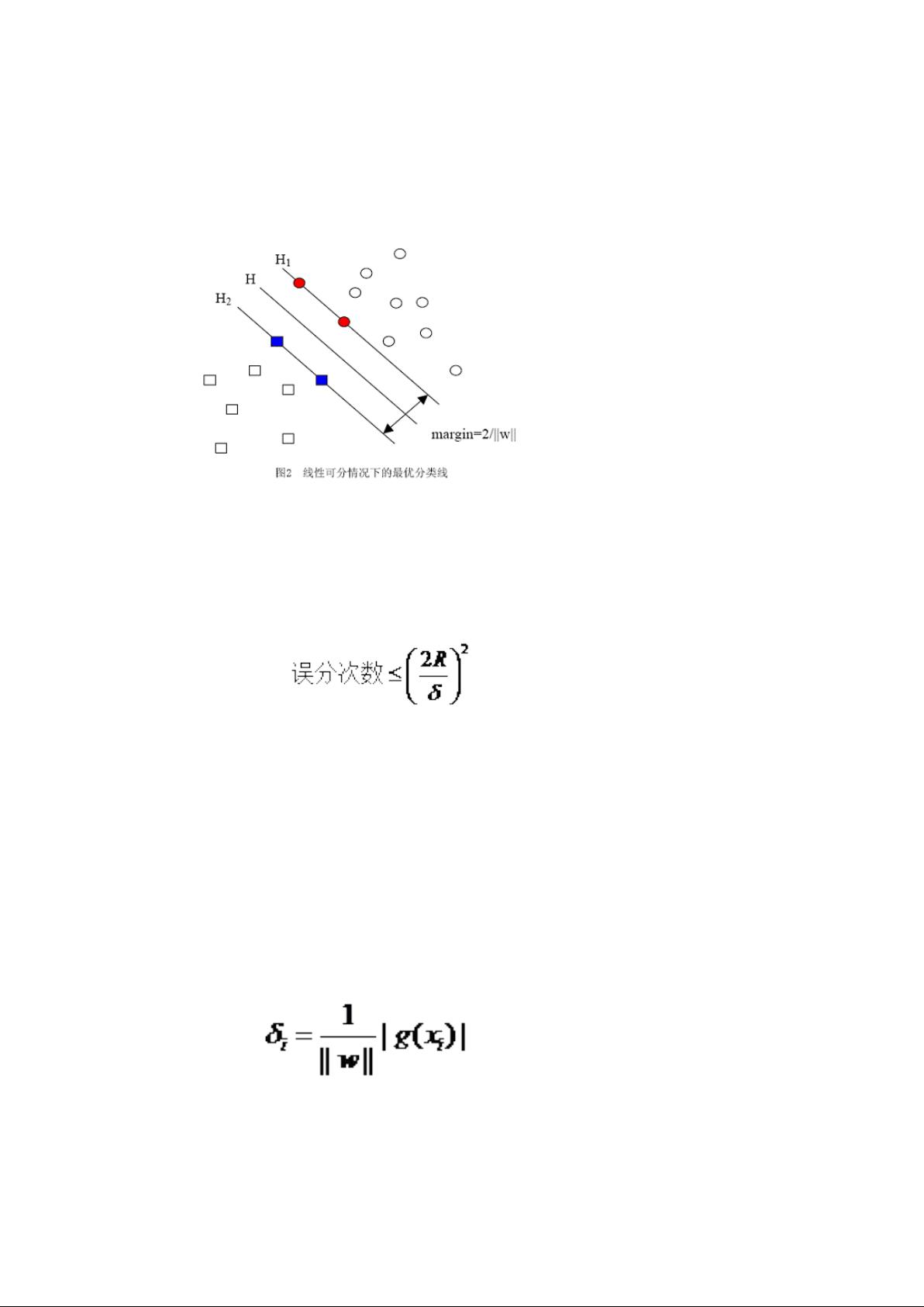
"支持向量机入门" 支持向量机（Support Vector Machine，简称SVM）是一种在机器学习领域广泛应用的算法，由Cortes和Vapnik于1995年首次提出。SVM在处理小样本、非线性和高维数据集时表现出显著的优势，不仅限于模式识别，还能应用于函数拟合等多种学习任务。SVM的核心理念是基于统计学习理论，特别是Vapnik-Chervonenkis（VC）维理论和结构风险最小化原则。 统计学习理论是由Vapnik发展的一套理论框架，它强调学习过程的理论基础，能够量化学习系统的性能，并预测其在未知数据上的泛化能力。相比传统的机器学习方法，统计学习更注重理论的严谨性和可预测性，避免了依赖于技巧和经验的盲目实践。 VC维是衡量一个函数类复杂度的关键指标，简单来说，它代表了该函数类能够正确分类的数据集的最大尺寸。VC维越高，意味着函数类越复杂，学习到的模型可能越容易过拟合。SVM的独特之处在于它并不直接依赖于输入数据的维度，即使在高维空间中，也能有效地找到分类超平面，这得益于引入了核函数的概念，它能够在原始低维空间中实现非线性决策边界。 结构风险最小化是SVM优化目标的关键概念，其核心思想是在训练过程中平衡模型的复杂度和准确性。通常，我们希望模型在训练数据上表现良好（低偏差），同时避免过度拟合（低方差）。结构风险最小化通过在训练误差和模型复杂度之间找到最佳平衡，从而提升模型的泛化能力。这意味着SVM不仅追求在训练集上的高准确率，更注重在未见过的数据上的预测性能。 在实际应用SVM时，选择合适的核函数至关重要，常见的核函数包括线性核、多项式核、高斯核（RBF）等。核函数的选择直接影响到SVM的分类效果，不同的核函数可以适应不同类型的数据分布和问题特性。 支持向量机是一个强大且灵活的机器学习工具，它的理论基础扎实，适用于多种复杂的学习任务。通过理解和支持向量机的核心原理，如统计学习理论、VC维和结构风险最小化，我们可以更好地利用SVM解决实际问题，并优化模型性能。在实践中，结合适当的特征工程和调参策略，SVM往往能够取得优秀的分类和回归结果。