微极理论在周期性蜂窝材料等效模型中的应用

"考虑位移连续和单胞力平衡的周期性蜂窝材料微极等效模型，通过微极理论对二维蜂窝材料进行广义连续介质等效，以模拟尺寸效应和边界层效应。该研究提出了新的推导微极本构关系的方法，保证位移连续和单胞力平衡条件，并通过数值模拟验证了等效参数的准确性。" 本文主要探讨了如何利用微极理论（Cosserat 介质理论）来构建周期性蜂窝材料的等效模型，以应对传统连续介质模型无法充分描述的尺寸效应和边界层效应。蜂窝材料因其超轻、强韧的特性在多领域有着广泛应用，但其复杂的结构使得精确的离散计算变得困难。因此，研究者们通常采用连续介质等效方法简化分析。 微极理论是解决这一问题的一种有效途径，它引入了转角自由度，能够更好地考虑材料内部的微小结构对整体性能的影响。在该研究中，作者阎军、牛斌和程耿东采用了微极理论，结合基于体积平均的均匀化方法，提出了一种新的策略，即在推导等效本构关系时同时满足位移连续和单胞力平衡条件。这种方法对于正六角形蜂窝材料尤为适用。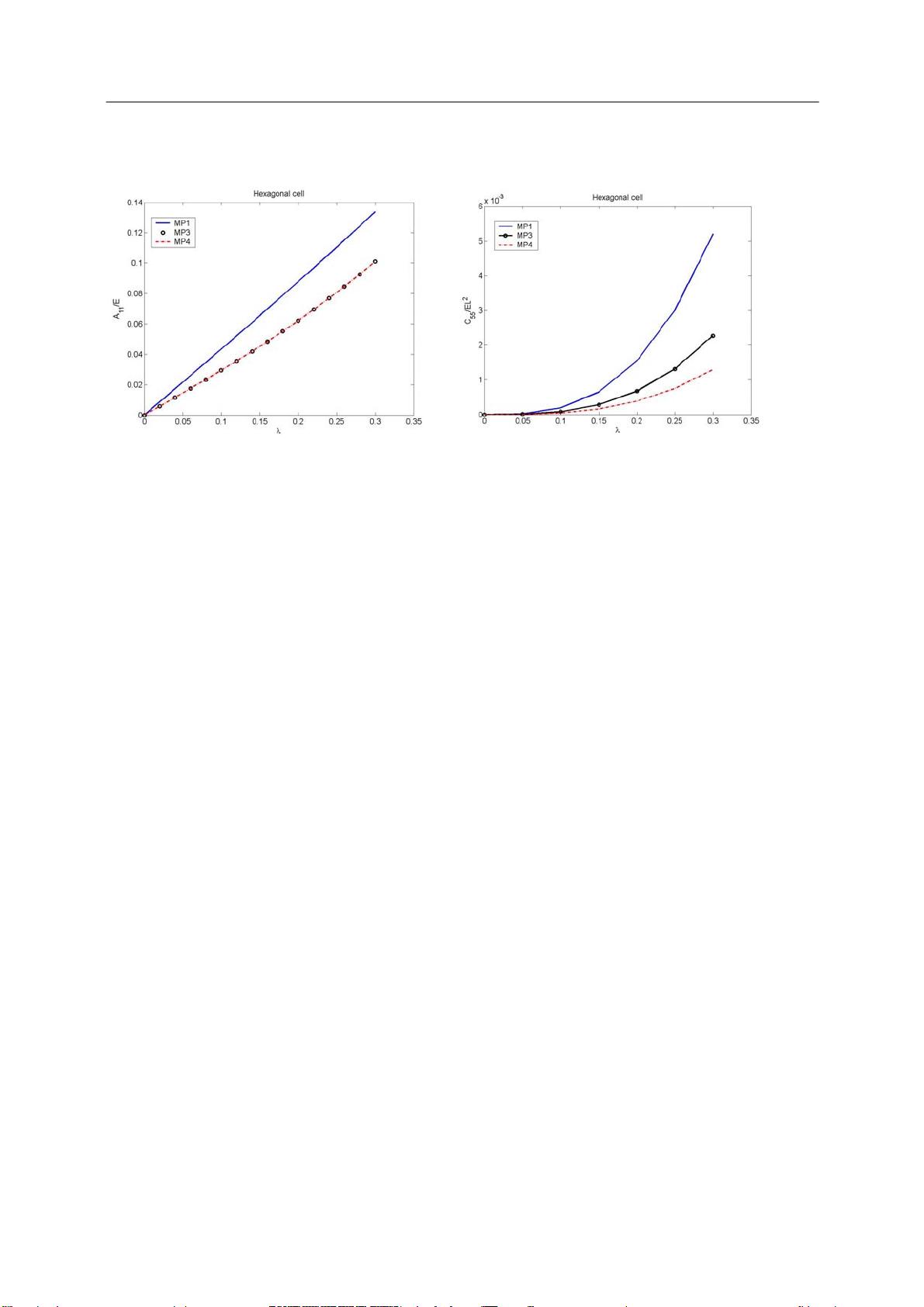 为了验证新模型的准确性，研究人员对由六角形蜂窝材料构成的结构进行了数值模拟，模拟中结构上表面受到均布剪力。他们对比了使用离散精确梁模型和不同等效微极本构参数的结果，以此确定最佳的微极参数值。数值模拟结果表明，本文提出的微极等效参数在加载点附近和边界区域的计算精度更高。 关键词包括蜂窝材料、微极介质、尺寸效应和等效属性。这些关键词强调了研究的核心内容，即如何通过微极理论捕捉蜂窝材料的尺寸相关力学特性，以及如何建立一个准确的等效模型来描述这些特性。 这项研究提供了一个创新的微极等效模型，它能够更好地捕捉周期性蜂窝材料的力学行为，特别是在处理尺寸效应和边界层效应时，提高了计算的精度和效率。这对于理解和设计基于蜂窝材料的复杂结构具有重要的理论和实践意义。