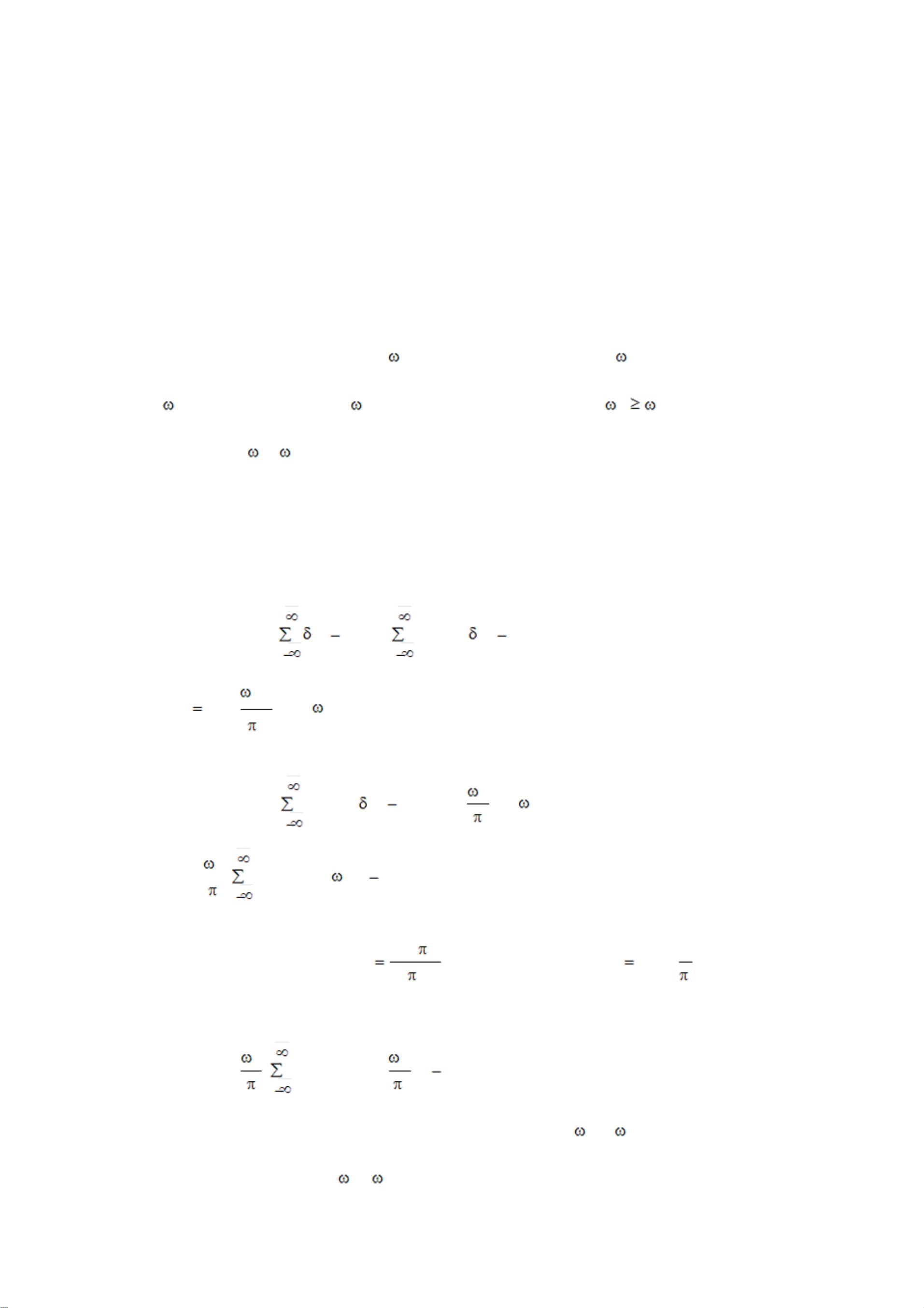MATLAB实现信号抽样与恢复：理论与实验

"该资源为MATLAB相关的实验指导材料，主要涉及信号的抽样与恢复。实验通过MATLAB实现连续信号的采样和重构，强调了抽样定理和信号重建的基本原理，并提供了具体的MATLAB代码示例。" 在信号处理领域，抽样和恢复是至关重要的步骤，特别是在数字信号处理中。本实验围绕这一主题，详细讲解了如何使用MATLAB进行操作。 首先，抽样定理是信号处理的基础，它指出如果一个带限信号f(t)的最高频率成分为fm，那么为了不失真地恢复这个信号，抽样频率fs必须大于2fm，即fs > 2fm。这被称为奈奎斯特定理。当fs < 2fm时，就会出现频率混叠现象，导致信号无法正确恢复。 信号的重建是通过将采样信号fs(t)经过一个理想低通滤波器h(t)来实现的。理想低通滤波器能有效地去除高于截止频率wc的高频成分，从而使经过滤波的采样信号能够重构出原始的连续信号f(t)。具体数学表示为f(t) = fs(t) * h(t)，其中fs(t)是抽样信号，h(t)是理想低通滤波器的响应。 实验中，选择了信号f(t) = Sa(t)作为被采样的信号，当抽样频率fs等于信号的两倍带宽，即fs = 2fm，这种情况下称为临界采样。理想低通滤波器的截止频率c设置为fm，这样可以有效地过滤掉不需要的频率成分。 实验内容包括两部分： 1. 验证抽样定理和信号重建的MATLAB程序，确保理论与实践的一致性。 2. 对于非严格带限信号f(t) = 0.5*(1+cos(t))*(u(t+π)-u(t-π))，尽管它的频谱主要集中在[0，2]之间，但可以根据精度需求近似带宽wm。实验对比了两种不同的抽样配置： - (1) wm = 2, wc = 1.2wm, Ts = 1; - (2) wm = 2, wc = 2, Ts = 2.5; 在这里，wm是信号的实际带宽，wc是低通滤波器的截止频率，Ts是抽样周期，1/Ts即为抽样频率。通过MATLAB实现这两种情况下的信号抽样和恢复，并计算原始信号f(t)与恢复信号的误差，以分析不同设置对恢复效果的影响。 在实际应用中，理解并掌握这些原理和方法对于设计有效的信号处理系统至关重要，尤其是在通信、图像处理和数据分析等领域。通过这样的实验，学习者可以更深入地理解信号抽样和恢复的过程，并掌握如何在MATLAB环境中实现这些操作。