多元分析：从聚类到市场细分的统计方法

"第29章 多元分析.pdf" 多元分析是统计学中处理多个变量关系的复杂方法，它是数理统计的重要组成部分，广泛应用于各个领域，包括工程、社会科学、生物学和企业管理等。由于实际问题中变量之间往往存在关联，不能孤立看待每个变量，因此需要通过多元分析来挖掘变量间的结构和关系。 聚类分析是多元分析中的一个重要分支，它的目的是对数据集中的对象进行分类，使其在同一个类别内的对象相似度较高，不同类别间对象的相似度较低。聚类分析可以应用于市场细分，帮助企业识别具有相似需求的消费者群体，以便制定更精准的市场策略。 聚类分析的基础是相似性度量，即如何量化对象之间的相似程度。在数学上，这通常通过计算距离来实现。对于包含多个变量的样本点，可以将其视为高维空间中的点，然后使用距离函数（如欧氏距离）来衡量两个点之间的距离。距离函数必须满足正定性（非负性）、对称性和三角不等式等基本性质，确保度量的合理性。 在多元分析中，特别是针对定量变量的聚类分析，最常使用的距离度量是欧氏距离（Euclidean distance），它基于每个变量的差异来计算两个样本点之间的直线距离。除此之外，还有曼哈顿距离（Manhattan distance）、切比雪夫距离（Chebyshev distance）以及马氏距离（Mahalanobis distance）等，这些距离度量在特定情况下各有优势，可以根据数据的特性和分析目的选择合适的度量方式。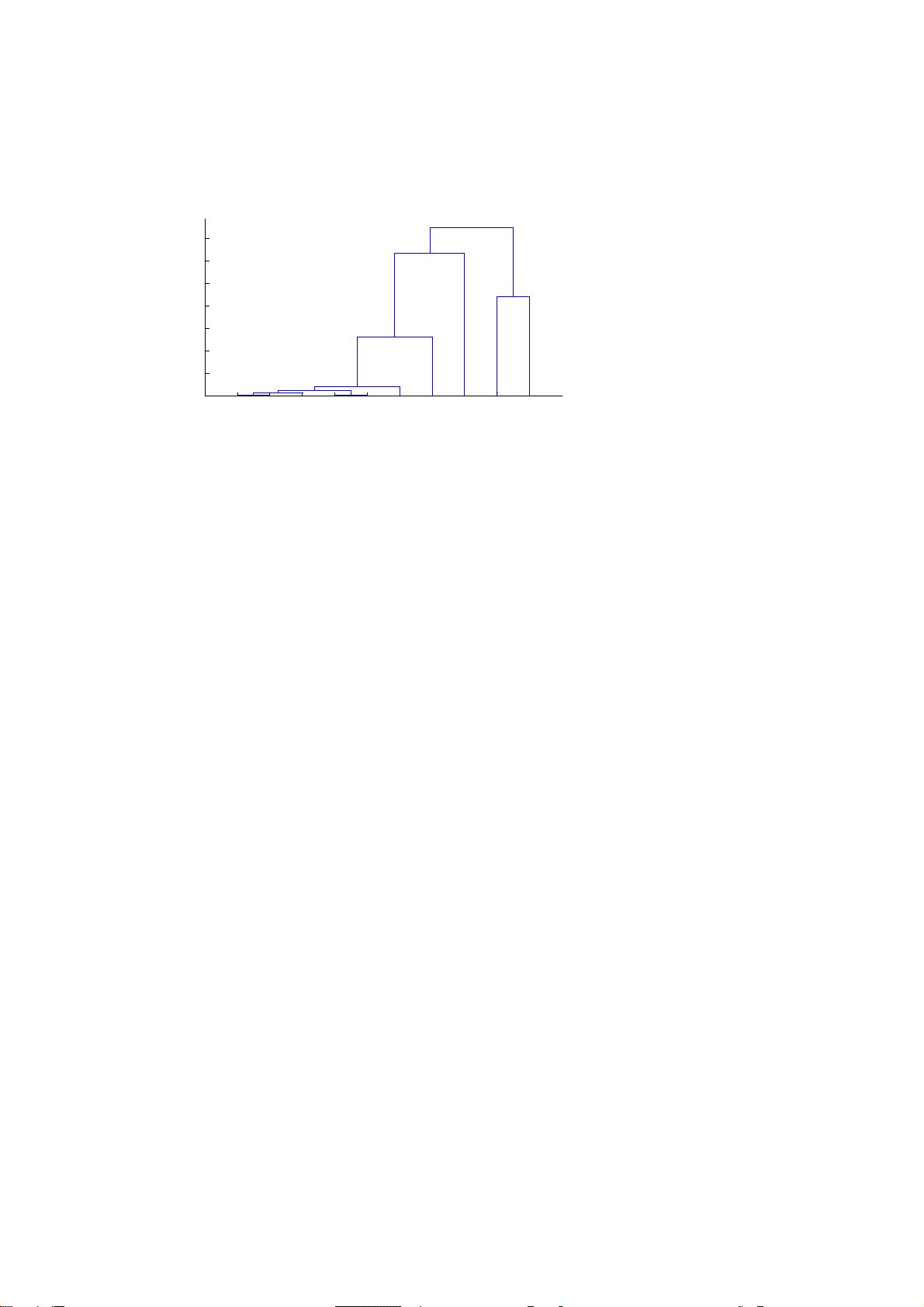 除了距离度量，聚类分析还包括不同的算法，如层次聚类（hierarchical clustering）和划分聚类（partitioning clustering，如K-means算法）。层次聚类可以形成树状结构（dendrogram），展示不同层次的聚类结果；而K-means算法则通过迭代优化，寻找最佳的类别划分，通常需要预先设定类别数量。 在实际应用中，多元分析还包括主成分分析（PCA）、判别分析（DA）、因子分析（FA）等多种技术，它们旨在降维、解释变量间的共线性、识别重要因素以及构建预测模型等。这些方法都有各自的适用场景，如PCA用于减少变量数量，保留主要信息；DA用于分类问题，找出区分不同类别的关键特征；FA则试图解释变量间的结构，找出潜在的因子。 多元分析是理解和解析复杂数据集的强大工具，它通过多种统计方法揭示隐藏在多变量数据背后的模式和关系，为企业决策、科学研究和理论探索提供有力支持。在实际操作中，选择合适的分析方法、合理地度量相似性和正确解读分析结果，是确保多元分析有效性的关键。