LeGall 5/3 小波变换详解与应用

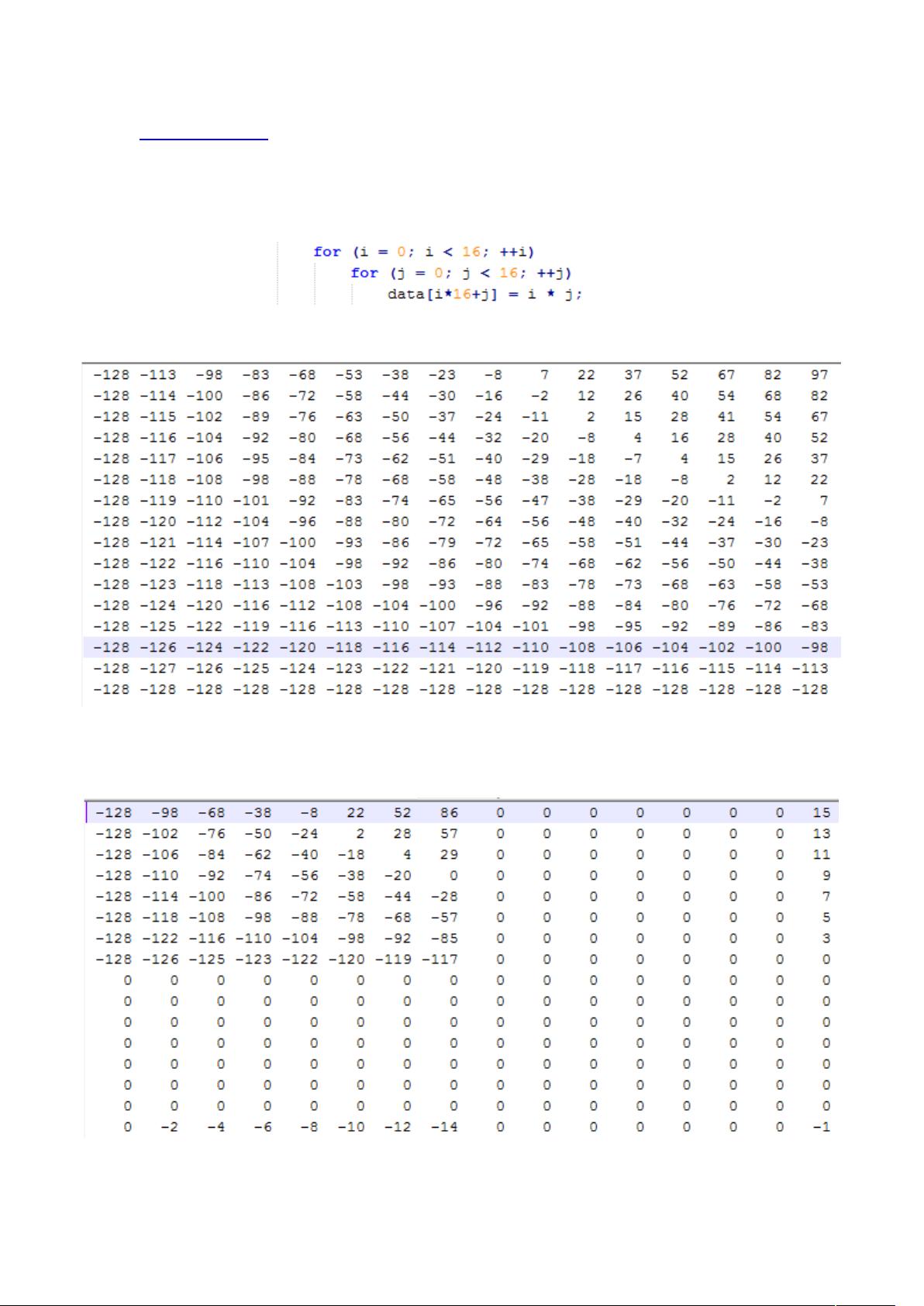
"db 5/3提升小波是一种用于信号和图像处理的小波变换方法，其中数字5代表分解滤波器的长度，而3表示重构滤波器的长度。这种小波基属于B样条正交小波系列，与经典的haar小波、daubechies小波和symlets小波并列。提升小波变换是小波分析中的一种高效算法，它通过一系列的滤波和上采样操作来进行信号的多分辨率分析。在本文中，我们以一个16x16的8位深度BMP图像为例，详细介绍了如何应用LeGall 5/3离散小波变换进行预处理和变换的过程。 首先，预处理步骤是将图像的像素值减去128，以确保像素值围绕0分布，变化范围在[-128, 127]之间。这一步是为了便于后续的计算和分析。 接着，执行LeGall 5/3离散小波变换，该变换通过四层进行，每层变换都会提供不同尺度下的图像信息。在第一层变换后，图像被分解为更细的细节和低频成分；第二层进一步细化了这些成分；第三层继续分解；到第四层时，图像已经变成了2x2的矩阵，这是数据量最小的形式，因此常用于简化计算和说明。 对于5/3小波变换的具体计算，以第四层的2x2矩阵为例，首先进行行变换。对每一行像素进行边界延拓，然后根据5/3提升小波的变换公式计算新的行值。以第一行为例，其原始像素值为[-128, 9, -128, 9, -128]，经过变换得到[-59, 137]。同样的过程应用于第二行，得到[-41, -84]。行变换后的结果组合形成新的矩阵。 接下来是列变换，对每一列像素应用相同的边界延拓和变换规则。以第一列为示例，原始像素值为[-59, -127]，经过5/3小波变换后得到[-79, -41]。第二列的变换结果为[95, -84]。这样，完成了整个第四层的5/3小波变换。 总结来说，db 5/3提升小波变换是一种有效的小波分析工具，通过预处理和多层变换，可以将图像或信号分解为不同频率成分，这对于压缩、降噪、特征提取等任务具有重要意义。在这个实例中，我们看到了如何具体实施这个过程，并理解了如何利用5/3提升小波进行图像的离散小波变换。"