EPnP方法：一种高效的摄像机外参数恢复方案

5星 · 超过95%的资源需积分: 9 44 浏览量更新于2024-11-01 收藏 1.09MB PDF 举报

"恢复摄像机外参数的经典文章EPnP，该文章详细介绍了EPnP方法，用于从3D到2D点对应关系中估计校准相机的姿态，具有线性时间复杂度，提高了计算效率，并能处理平面和非平面配置的情况。" 在计算机视觉领域，摄像机外参数是描述摄像机在三维空间中位置和方向的关键信息。EPnP（Efficient Perspective-n-Point）方法是解决PnP问题（Perspective-n-Point）的一种高效算法，即从n个3D点及其对应的2D投影点中估计摄像机的外参数。传统的PnP求解方法通常基于迭代优化，如Levenberg-Marquardt算法，其时间复杂度较高，随着n的增加，计算量显著增大，而EPnP算法的提出改变了这一状况。文章"EPnP: An Accurate O(n) Solution to the PnP Problem"由Vincent Lepetit、Francesc Moreno-Noguer和Pascal Fua共同撰写，于2008年发表在《International Journal of Computer Vision》上。作者提出了一个非迭代的解决方案，其计算复杂度与n成线性关系，显著降低了计算负担，且在效率提升的同时，精度并未下降。 EPnP的核心思想是将每个3D点表示为四个虚拟控制点的加权和。这样，问题就转化为估计这些控制点在摄像机坐标系中的坐标，这可以通过解析方式完成。首先，构造一个12x12的矩阵，并求解其特征向量。然后，通过解一组二次方程来确定控制点的权重，从而找到正确的摄像机姿态。如果需要更高的精度，还可以利用闭式解的输出进行进一步优化。此外，EPnP算法能够适应各种场景，无论是在平面上还是非平面上的点对应，都能得到准确的结果。这使得它在实际应用中，如机器人导航、增强现实、3D重建等领域具有广泛的应用潜力。 EPnP算法通过创新的数学建模和解析解法，为解决PnP问题提供了新的思路，它的高效性和准确性使其成为计算机视觉领域的一个重要里程碑。对于需要快速准确地估计摄像机姿态的系统来说，EPnP算法是一个非常有价值的工具。

Int J Comput Vis

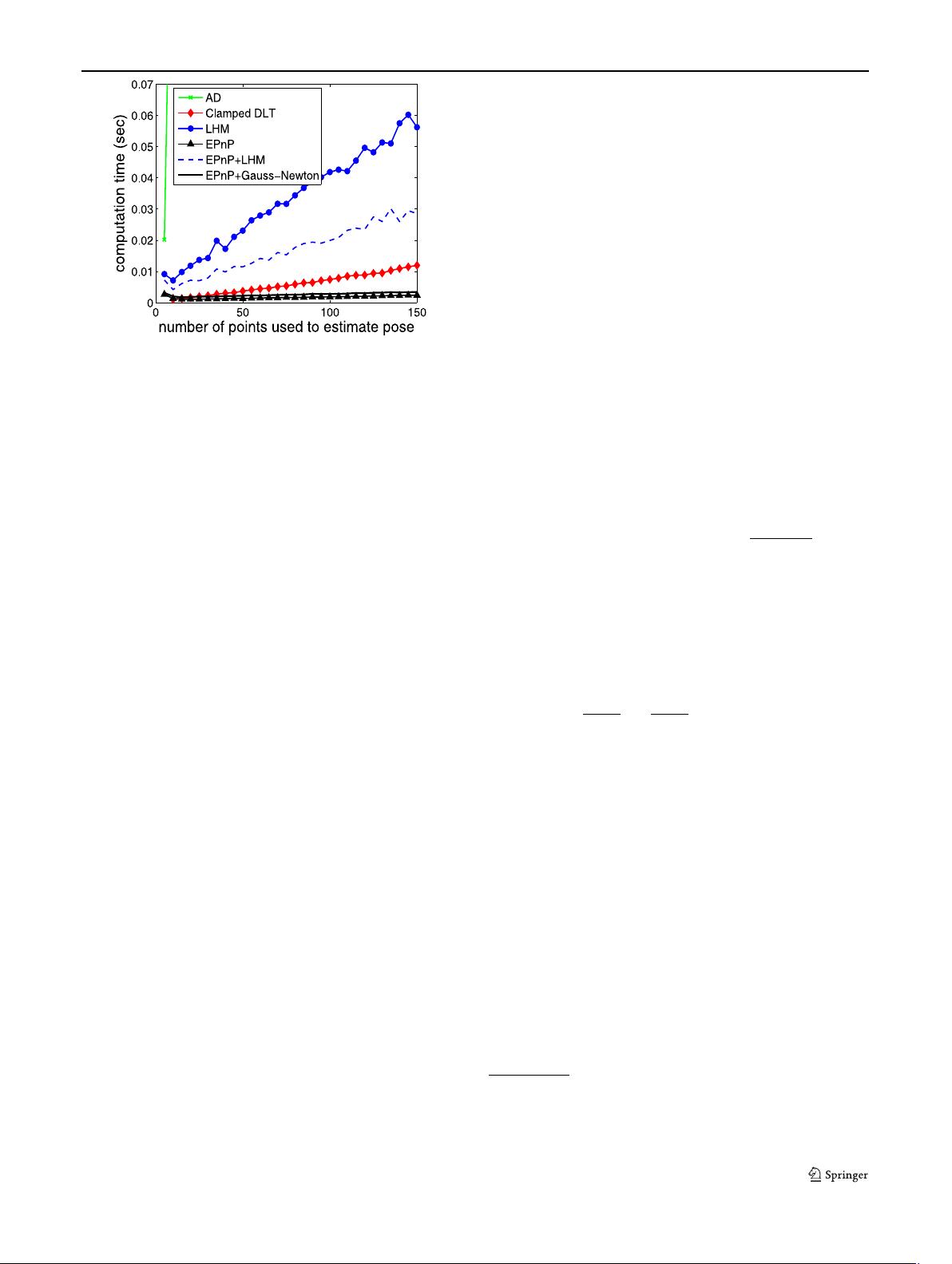
Fig. 2 Comparing computation times of our method against the

state-of-the-art ones introduced in Fig. 1. The computation times of

a MATLAB implementation on a standard PC, are plotted as a func-

tion of the number of correspondences. Our method is both more ac-

curate—see Fig. 1—and faster than the other non-iterative ones, espe-

cially for large amounts of noise, and is almost as accurate as the iter-

ative LHM. Furthermore, if maximal precision is required, the output

of our algorithm can be used to initialize a Gauss-Newton optimization

procedure which requires a negligible amount of additional time

urations, which cause problems for some methods as dis-

cussed in Oberkampf et al. (1996), Schweighofer and Pinz

(2006), by using three control points instead of four.

In the remainder of the paper, we ﬁrst discuss related

work focusing on accuracy and computational complexity.

We then introduce our new formulation and derive our sys-

tem of linear and quadratic equations. Finally, we compare

our method against the state-of-the-art ones using synthetic

data and demonstrate it using real data. This paper is an

expanded version of that in Moreno-Noguer et al. (2007),

where a ﬁnal Gauss-Newton optimization is added to the

original algorithm. In Sect. 4 we show that optimizing over

a reduced number of parameters, the accuracy of the closed-

solution proposed in Moreno-Noguer et al. (2007) is con-

siderably improved with almost no additional computational

cost.

2 Related Work

There is an immense body of literature on pose estimation

from point correspondences and, here, we focus on non-

iterative approaches since our method falls in this category.

In addition, we will also introduce the Lu et al. (2000) it-

erative method, which yields very good results and against

which we compare our own approach.

Most of the non-iterative approaches, if not all of them,

proceed by ﬁrst estimating the points 3D positions in the

camera coordinate system by solving for the points depths.

It is then easy to retrieve the camera position and orientation

as the Euclidean motion that aligns these positions on the

given coordinates in the world coordinate system (Horn et

al. 1988;Arunetal.1987; Umeyama 1991).

The P3P case has been extensively studied in the liter-

ature, and many closed form solutions have been proposed

such as Dhome et al. (1989), Fischler and Bolles (1981),

Gao et al. (2003), Haralick et al. (1991), Quan and Lan

(1999). It typically involves solving for the roots of an eight-

degree polynomial with only even terms, yielding up to four

solutions in general, so that a fourth point is needed for

disambiguation. Fisher and Bolles (1981) reduced the P4P

problem to the P3P one by taking subsets of three points

and checking consistency. Similarly, Horaud et al. (1989)

reduced the P4P to a 3-line problem. For the 4 and 5 points

problem, Triggs (1999) derived a system of quadratic poly-

nomials, which solves using multiresultant theory. However,

as pointed out in Ansar and Daniilidis (2003), this does not

perform well for larger number of points.

Even if four correspondences are sufﬁcient in general

to estimate the pose, it is nonetheless desirable to consider

larger point sets to introduce redundancy and reduce the sen-

sitivity to noise. To do so, Quan and Lan (1999) consider

triplets of points and for each one derive four-degree poly-

nomials in the unknown point depths. The coefﬁcients of

these polynomials are then arranged in a

(n−1)(n−2)

×5ma-

trix and singular value decomposition (SVD) is used to es-

timate the unknown depths. This method is repeated for all

of the n points and therefore involves O(n

) operations.

should be noted that, even if it is not done in Quan and Lan

(1999), this complexity could be reduced to O(n

) by apply-

ing the same trick as we do when performing the SVD, but

even then, it would remain slower than our method. Ansar

and Daniilidis (2003) derive a set of quadratic equations

arranged in a

n(n−1)

× (

n(n+1)

+ 1) linear system, which,

as formulated in the paper, requires O(n

) operations to be

solved. They show their approach performs better than Quan

and Lan (1999).

The complexity of the previous two approaches stems

from the fact that quadratic terms are introduced from the

inter-point distances constraints. The linearization of these

equations produces additional parameters, which increase

the complexity of the system. Fiore’s method (Fiore 2001)

avoids the need for these constraints: He initially forms a

set of linear equations from which the world to camera rota-

tion and translation parameters are eliminated, allowing the

direct recovery of the point depths without considering the

inter-point distances. This procedure allows the estimation

of the camera pose in O(n

) operations, which makes real-

time performance possible for large n. Unfortunately, ignor-

ing nonlinear constraints produces poor results in the pres-

ence of noise (Ansar and Daniilidis 2003).

Following Golub and Van Loan (1996), we consider that the SVD

for a m × n matrix can be computed by a O(4m

n + 8mn

+ 9n

)

algorithm.

剩余11页未读，继续阅读

hwb506

粉丝: 38

EPnP方法：一种高效的摄像机外参数恢复方案

EPnP算法实现：多摄像头参数恢复技术

MATLAB实现EPnP算法：快速求解相机姿态

AR相机姿态估计：EPnP+LM算法优化与实验分析

摄像机外参数标定（位姿估计 pose estimation）的经典文章和代码 EPNP

pnp恢复摄像机外参数及其源代码

EPnP_matlab.zip_EPnP_epnp matlab_matlab 摄像头_多摄像头_多摄像机

epnp.rar_EPnP_EPnP算法

epnp:epnp 的柳絮化

EPNP.zip_EPnP算法_EPnP算法流程_Epnp姿态估计_epnp matlab_姿态估计

EPnP_Eigen:用Eigen实现EPnP算法

最新资源