MATLAB中的龙格-库塔法：求解微分方程与稳定性分析

龙格库塔法是一种在数值分析领域广泛应用的高级单步积分方法，尤其在求解常微分方程组时，因其高精度和误差控制能力而受到工程师的青睐。本文将详细介绍如何在MATLAB环境下利用龙格库塔算法进行微分方程的数值求解，包括基本概念和实际操作步骤。 首先，MATLAB是一个强大的数学软件包，由MathWorks公司开发，它不仅提供了高效的矩阵运算功能，还支持图形可视化编程，使得复杂问题的解决变得直观且高效。在MATLAB中，用户可以通过矩阵形式输入方程组，例如定义函数`equition(t,x)`来表示方程结构，其中变量`q(1)`和`q(2)`分别对应微分方程中的应变量x和y。 针对经典的一阶欧拉方法，龙格库塔法通过在每个时间步长`h`内计算一个或多个点的斜率来提高精度。对于一阶精度，公式为`yi+1 = yi + h * K1`，其中`K1`是当前点的斜率估计。在二阶精度的改进欧拉公式中，算法使用了点`xi`处的`K1`和`xi+1`处的`K2`的算术平均值来估算平均斜率`K*`，即`yi+1 = yi + h * (K1 + K2) / 2`。 随着阶数的提升，龙格库塔算法会采用更多的斜率值来计算下一个时间点，如三阶、四阶等，这有助于进一步减小误差。在实际编程中，MATLAB的向量化特性使得处理矩阵和计算斜率变得简单，相比C++中对数组元素位置的精确指定，MATLAB的语法更加简洁直观。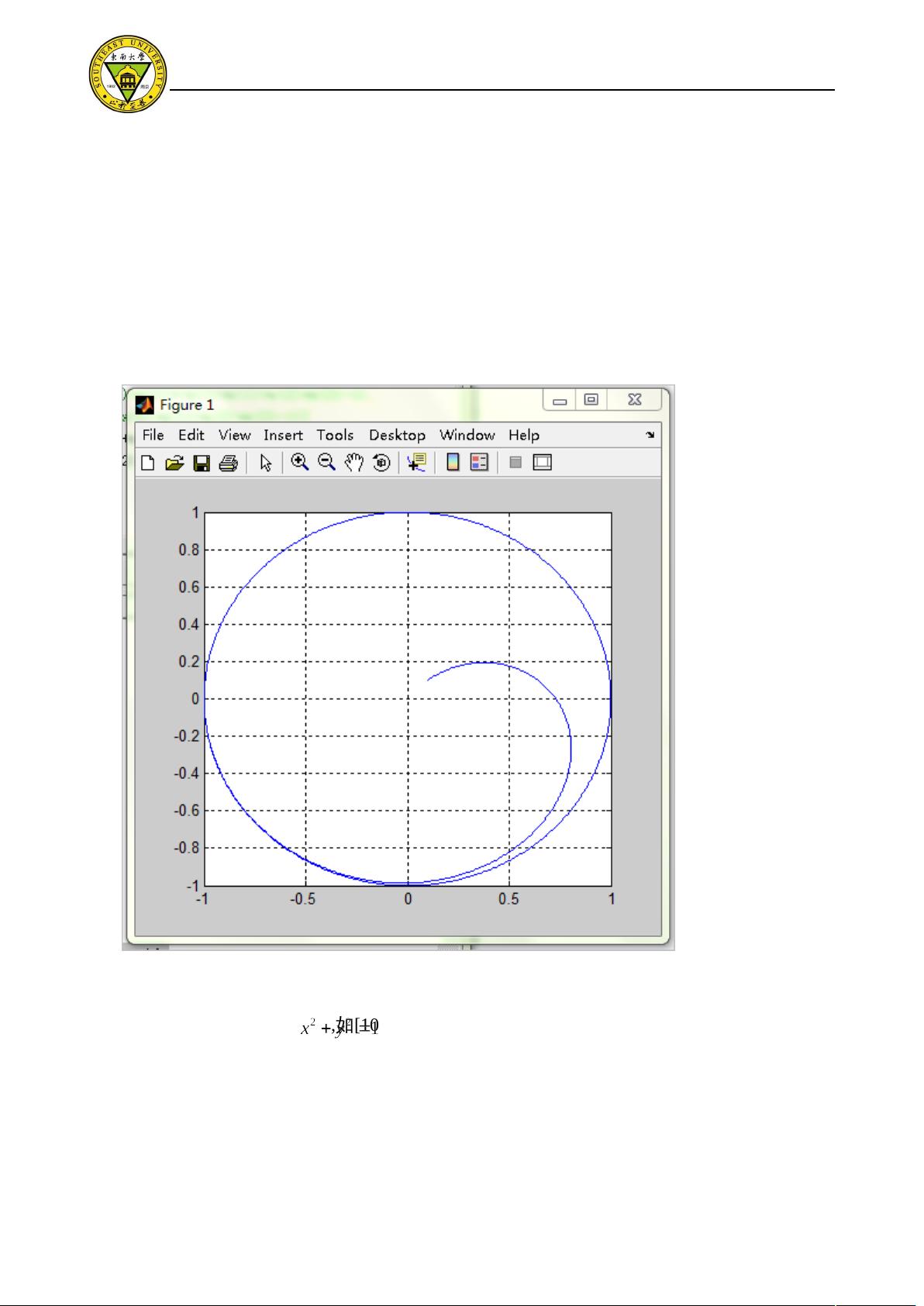 文章还可能探讨了范德波尔方程的应用，这是一种典型非线性微分方程，用于研究混沌系统中的奇怪吸引子。在MATLAB中，通过实现龙格库塔算法并结合图形可视化，可以有效地模拟和研究这些复杂的动态行为。 本文将深入解析如何在MATLAB中使用龙格库塔法求解微分方程，包括算法原理、代码实现以及如何通过这个工具处理和理解像范德波尔方程这样的复杂系统。这对于数值分析的实践者来说，是一个实用且重要的技能。