粒子滤波算法在MATLAB中的应用与二维目标跟踪

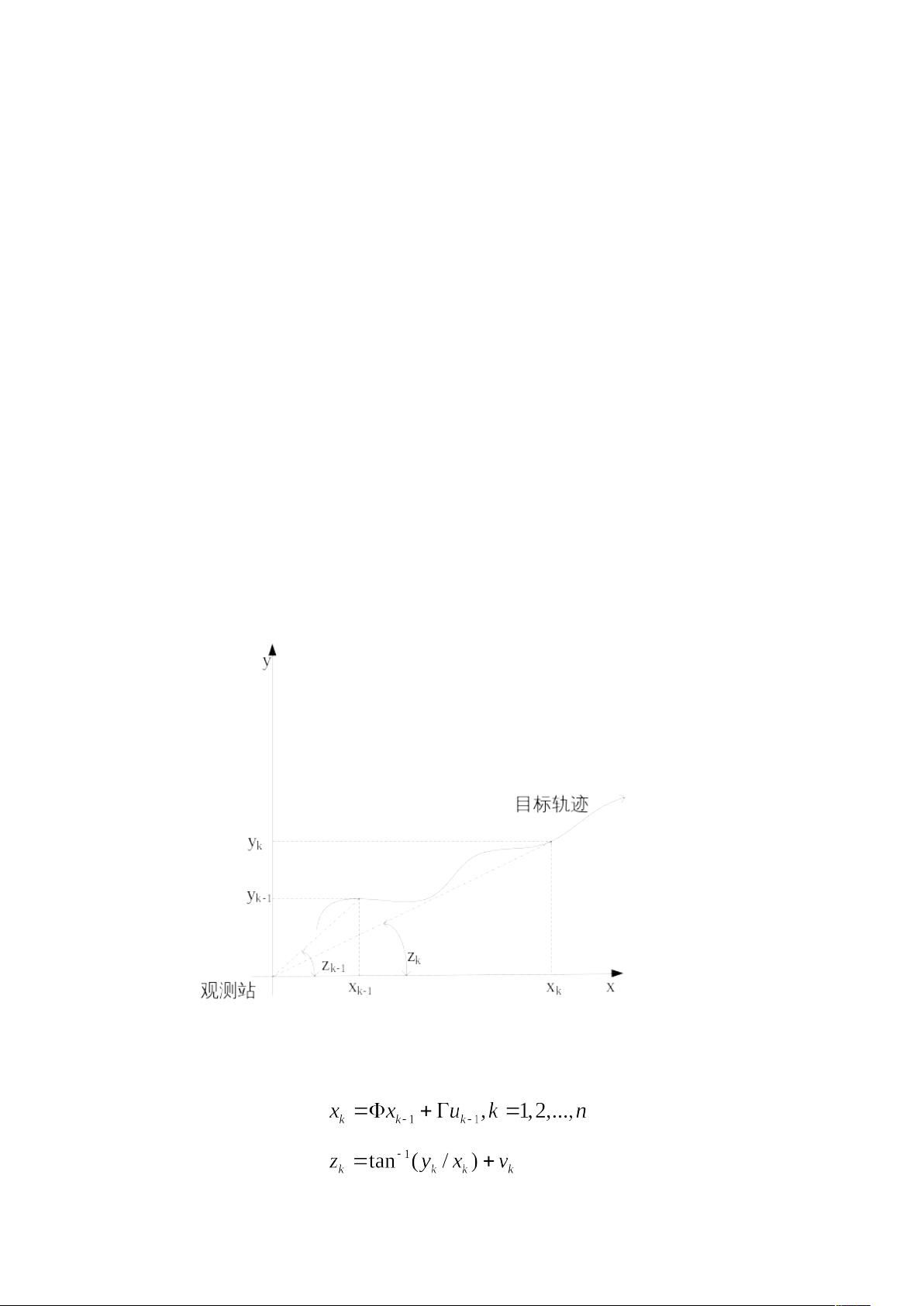
"粒子滤波matlab - 入门编程 - 被动定位系统 - 目标跟踪 - SIRF算法" 粒子滤波是一种用于非线性、非高斯动态系统的概率滤波方法，尤其适用于那些传统卡尔曼滤波无法有效处理的问题。在MATLAB中实现粒子滤波，可以帮助理解其基本原理并应用于实际项目，例如目标的被动跟踪。 在被动定位系统中，目标的跟踪通常是基于角测量进行的，而不依赖于距离信息。由于系统的观测性和非线性特性，递推滤波算法，如粒子滤波，成为了理想的解决方案。粒子滤波的核心在于通过一组随机样本，即“粒子”，来近似表示系统的后验概率分布。算法主要包括三个主要步骤： 1. **采样**：根据系统状态转移模型，生成新的粒子集合。在二维纯方位目标跟踪模型中，这涉及到根据上一时刻的状态（位置和速度）生成k时刻的粒子。 2. **权值计算**：根据观测数据更新每个粒子的权重。观测模型（通常包含测量噪声）用于计算每个粒子与实际观测的匹配程度，从而确定其权重。 3. **重采样**：根据粒子的权重重新生成新的粒子集合。低权重的粒子被抛弃，高权重的粒子被复制以形成新的种群，确保重要粒子对状态估计的贡献得以保留。 SIRF（Sample Importance Resampling Filter）算法就是一种基础的粒子滤波实现。在被动定位系统的二维纯方位目标跟踪中，SIRF算法的具体步骤如下： 1. **采样阶段**：利用状态转移模型（1.1）生成k时刻的粒子集合，其中考虑了系统的状态（位置和速度）以及系统噪声。 2. **权值计算阶段**：使用先验概率密度函数作为重要性函数，计算每个粒子的新权重，这些权重反映了粒子与观测值的匹配程度。 3. **重采样阶段**：根据计算出的权重，执行重采样过程，确保重要的粒子被保留下来，而低权重的粒子被新的粒子替代。 在实际应用中，还需要考虑一些优化策略，如避免粒子退化（所有粒子权重趋近于0或1的情况），以及提高计算效率的方法，如使用重要性密度的近似和减少粒子数量等。 在MATLAB中，可以构建相应的仿真环境，模拟目标的运动，设置观测模型和系统噪声，并实现粒子滤波算法来跟踪目标。通过调整参数和比较不同滤波器的性能，可以深入理解粒子滤波的优势和局限性，这对于理解和改进滤波技术至关重要。