MIMO relay网络优化：MMSE与SNR设计扩展

需积分: 3 137 浏览量更新于2025-01-03 收藏 656KB PDF 举报

本文档深入探讨了"优化多输入-多输出(MIMO)中继网络"的主题，发表在2008年10月的IEEE Transactions on Signal Processing上，作者为Alireza Shahan Behbahani、Ricardo Merched和Ahmed M. Eltawil，均为IEEE成员。随着无线传感器网络中有限的尺寸和功率资源对天线数量的限制日益突出，信号处理技术在这些网络中的作用变得至关重要。研究关注的是在给定的多天线中继架构下，如何通过优化实现效率最大化。首先，论文扩展了先前关于最小均方误差(MMSE)和信噪比(SNR)优化的设计方法，将其应用于MIMO环境。在这种情况下，源、中继节点和目的地都配备了多个天线，这使得系统性能显著提升，因为多天线技术可以提供空间复用和分集增益。针对功率受限的情况，论文探讨了最大信噪比(SNR)的解决方案，采用零forcing (ZF)准则来减小干扰。这种技术通过调整信号传输，确保信号质量在满足功率预算的同时达到最优。此外，文中还关注了在接收端设计具有特定目标信噪比和功率约束的近似MMSE均衡器，以进一步提高接收信号的质量和解码性能。传输速率是另一个关键性能指标，文章旨在最大化源与目的地之间的数据传输速度，考虑到中继节点的协同工作和可能存在的多径衰落。通过优化这些参数，作者旨在找到在实际应用中既能保证信号质量又能有效利用资源的最佳操作策略。总结来说，这篇论文对于那些寻求在MIMO中继网络中实现高效能、低能耗和高可靠性的无线通信系统设计者来说，提供了宝贵的理论指导和技术参考。通过深入分析和优化算法，它揭示了在复杂无线环境中如何通过合理配置和信号处理来克服挑战，以提升整体系统的性能和效率。

5064 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 56, NO. 10, OCTOBER 2008

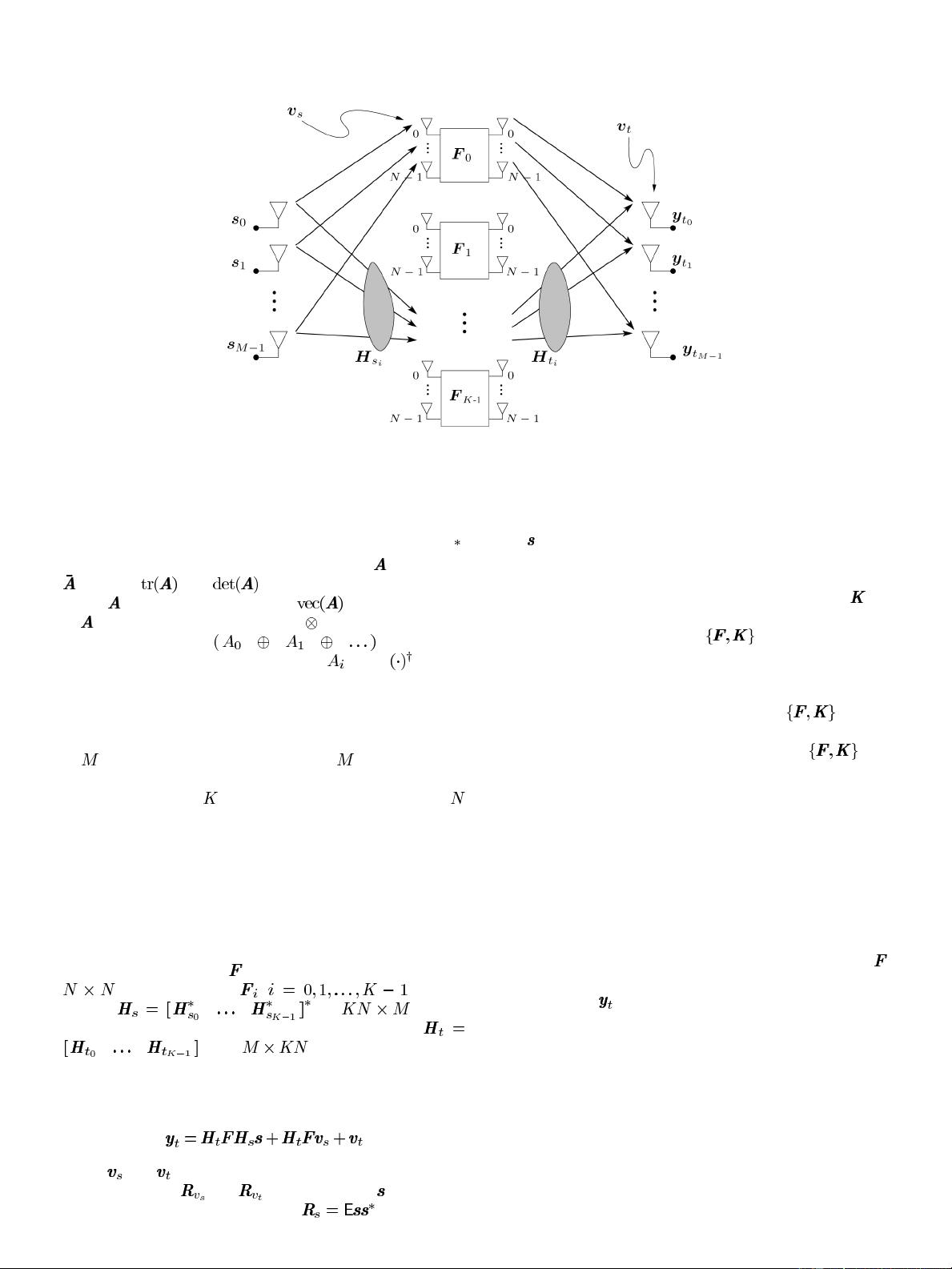
Fig. 1. MIMO relay architecture with intrarelay cooperation.

Notation

We shall use lower case for vectors, while capital letters for

matrices. The complex transposition operator is deﬁned as

while the conjugate of the elements of a matrix

, is given by

. Also the , and are the trace and determinant of

matrix

respectively. The operation stacks the columns

into a single column vector, and denotes the Kronecker

product. We denote by

a block diag-

onal matrix with block elements given by

. Also, denotes

the pseudoinverse.

II. P

ROBLEM FORMULATION

Fig. 1 illustrates a MIMO wireless sensor network consisting

transmit antennas at the source and receive antennas

at the destination. We consider an amplify-and-forward relay

scheme consisting of

relays, each relay is equipped with

transmit/receive antennas. In the subsequent discussions we de-

rive relations between the number of transmit and receive an-

tennas for each condition to have a unique solution. As long

as these relations are honored, having unequal numbers of re-

ceive and transmit antennas are possible, and would affect the

diversity gain of the system. For the purposes of this paper

we focus on the case where the number of transmit and re-

ceive antennas are equal. The relay matrix is represented by

a block diagonal matrix

, where each block is given by a

relay gain matrix , . We de-

note by

the channel

matrix between the source and the relay nodes, while

is the channel matrix between

the relay sensors and the destination. The channel matrices are

memoryless and a quasi-static fading condition is assumed. The

received signal is modeled as

(1)

where

and are additive Gaussian noise (AGN) with co-

variance matrixes

and respectively and is the trans-

mitted signal with covariance matrix

. A two-phase

(two-hop) protocol is used to transmit data from the source to the

receiver. In the ﬁrst phase (hop) the source broadcasts a signal

vector

towards the relay sensors. In the second phase, the relay

sensors retransmit the information to the destination. At the re-

ceiver, depending on the design criterion, one can further em-

ploy a MIMO equalizer, which we shall denote later by

,in

order to compensate for the effect of the overall MIMO channel.

In the latter, the goal is to design

both separately and

jointly, possibly considering a power constraint. We investigate

the performance of a MIMO relay network under the following

scenarios.

1) First, the relay matrix and equalizer pair

are de-

signed under a MMSE criterion, considering two distinct

cases: i) without power constraint, where

are

designed in two independent steps; ii) under an output

power constraint, where the relays are selected such that

the overall MMSE is minimized. Finally, we present a

closed-form solution for the case of global power con-

straint at the relays albeit for the special case of minimizing

the MSE of a SISO system. A similar approach was con-

sidered in [18], where the authors maximize the received

signal power. However in the latter, a closed form solution

was found only for high SNR situations.

2) Second, without considering any predetermined MIMO

decoder (equalizer), we design the optimal relay matrix

such that it maximizes the output SNR without post-equal-

ization (see

in Fig. 1). This is achieved under a ZF

criterion, ﬁrst with a speciﬁed target output SNR. Then, by

relaxing the target SNR condition, a total power constraint

for the relays is enforced. Note that in such cases, the role

of the relays is to provide equalization for the underlying

forward and backward channels. Observe also that in [16],

a similar ZF technique is considered, where each relay

performs ZF on its local backward and forward channels,

albeit without considering the effect of noise at the relays.

The proposed ZF approach outperforms the one of [16],

however with higher complexity since each relay requires

knowledge on the entire backward channel as well as its

Authorized licensed use limited to: National Central University. Downloaded on December 26, 2008 at 01:37 from IEEE Xplore. Restrictions apply.

剩余11页未读，继续阅读

FSTseng

粉丝: 0
资源: 7

MIMO relay网络优化：MMSE与SNR设计扩展

Babel插件优化指南：babel-preset-optimizations与babel-minify

Python库 emzed_optimizations最新版本下载指南

"Android 12新特性全面解析：功能升级、设计优化，全方位探索

Large-Scale Deep Learning Optimizations—A Comprehensive

Design and Evaluation of Dynamic Optimizations for a Java Just-In-Time Compiler

Embedded Linux optimizations

golang-optimizations

Power-Saving Optimizations

Z-Buffer Optimizations

eClass Optimizations-crx插件

最新资源