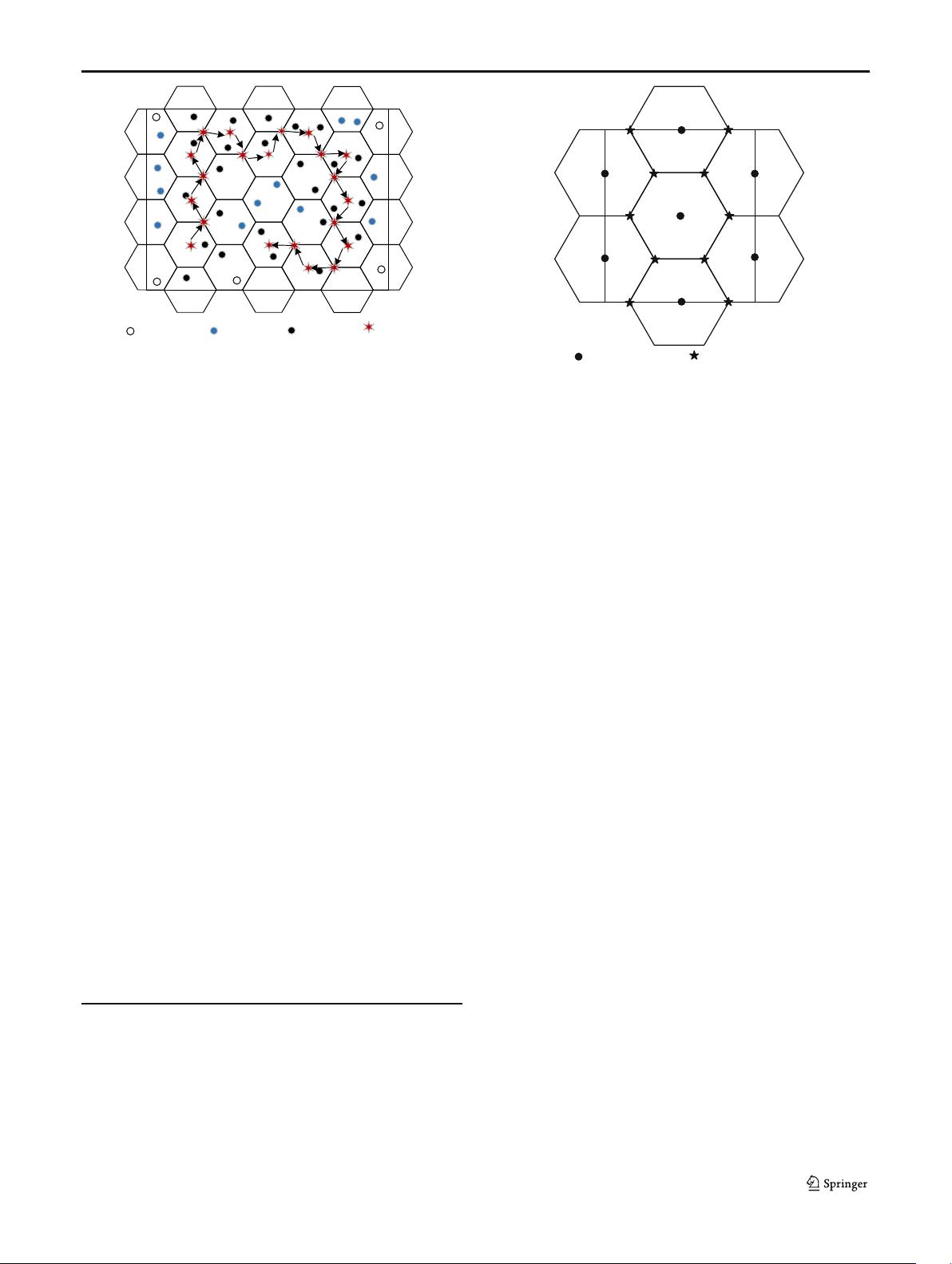
AsshowninFig.1, there are beacon node, anchor sensor
nodes, guide sensor nodes and unlocated sensor nodes. In the
area sensor nodes are randomly distributed and need to know
their own locations. Meanwhile, in order to reduce the system
cost and energy consumption, a mobile beacon node assists to
locate the sensor nodes. Beacon node stays at the initial center
of grid, selects an unstayed vertex of grid to move to. It stays at
the location and sends its location information packet some
time, and moves to another unstayed center of grid which has
the vertex. Because three adjacent locations are not collinear,
when beacon node selects sojourn location, it deletes the loca-
tion which is collinear with last two locations. Beacon node
keeps moving and sending its location information packet until
it reaches maximum movement distance. Sensor nodes receive
the information of more than 3 non-collinear locations of bea-
con node, collect RSSI value during communication, use
Kalman filter to reduce communication noise, calculate their
own coordinates by maximum likelihood estimation algorithm,
mark themselves as anchor sensor nodes and broadcast their
locations to assist other sensor nodes which are not located by
beacon node. The sensor nodes whose locations are not located
by beacon node, estimate their locations based on the location
information of beacon node and anchor sensor nodes in the
vicinity, mark themselves as guide sensor nodes, send their
locations to beacon node and guide the movement of beacon
node. Both anchor sensor nodes and guide sensor nodes obtain
their locations, but the locations of anchor sensor nodes are
more precise than the locations of guide sensor nodes.
As shown in Fig. 2, when WSNs start, beacon node needs
to divide its movement area into a number of hexagonal grids
of uniform size [25], and needs to number all hexagonal grids
and vertices of the grids in the movement area according to the
principle of from left to right and from bottom to top. For
example, grid(2,1) represents a hexagonal grid which is in
column 2 from the left and row 1 from the bottom.
Ding(2,2) represents the vertex which is in column 2 from
the left, and row 2 from the bottom. But NLA_MB algorithm
needs to solve the following three problems. First, how to use
mathematical formulas to express the constraint conditions,
such as movement path constraint, movement distance con-
straint, etc. How to establish the optimization model of node
localization errors. Second, how do sensor nodes calculate
their own coordinates with beacon node’ movement and loca-
tion information of anchor sensor nodes? Third, how beacon
node use heuristic algorithm to solve the optimization model
approximately and obtain movement path? The specific solu-
tions to the three problems are as follows.
2.1 Constraint analysis and optimization model
establishment
2.1.1 Constraint analysis
As shown in Fig. 1 and Fig. 2, if current sojourn location of
beacon node is center of grid, next sojourn location is vertex
of the grid. If current sojourn location is vertex of grid, next
sojourn location is center of the grid which has the vertex.
Then when current sojourn location of beacon node is center
of grid, the next optional location set is
N
g
¼
ding 1; 2j−1ðÞ; ding 1; 2 jðÞ; ding 1; 2 j þ 1ðÞfgp
g
¼ p 1; jðÞ
ding n−1; 2j−1ðÞ; ding n−1; 2jðÞ; ding n−1; 2j þ 1ðÞ
fg
p
g
¼ pn; jðÞ
ding i−1; 1ðÞ; ding i−1; 2ðÞ; ding i; 1ðÞ; ding i; 2ðÞ
fg
p
g
¼ pi; 1ðÞand i is even
ding i−1; 2mðÞ; ding i−1; 2m þ 1ðÞ; ding i; 2mðÞ; ding i; 2m þ 1ðÞ
fg
p
g
¼ pi; m þ 1ðÞand i is even
ding i−1; 2j‐2
ðÞ
; ding i−1; 2 j−1
ðÞ
; ding i−1; 2 j
ðÞ
; ding i; 2j‐2
ðÞ
; ding i; 2 j−1
ðÞ
; ding i; 2 j
ðÞ
f g others when i is even
ding i−1; 2j‐1ðÞ; ding i−1; 2 jðÞ; ding i−1; 2j þ 1ðÞ; ding i; 2j‐1ðÞ; di
ng i; 2jðÞ; ding i; 2 j þ 1ðÞ
f g
others when i is odd
8
>
>
>
>
>
>
<
>
>
>
>
>
>
:
ð1Þ
S8
guide
sensor node
beacon
node
unlocated
sensor node
anchor
sensor node
Fig. 1 Principle of NLA_MB algorithm
grid(1, 1)
grid(1, 2)
grid(2, 2)
grid(2, 3)
grid(2, 1)
grid(3, 1)
grid(3, 2)
ding(1,1)
ding(1,2)
ding(1,3)
ding(1,4)
ding(1,5)
ding(2,1)
ding(2,2)
ding(2,3)
ding(2,4)
ding(2,5)
center of grid
vertex of grid
Fig. 2 Numbering method
Peer-to-Peer Netw. Appl.









