机器学习入门：线性回归详解与实践

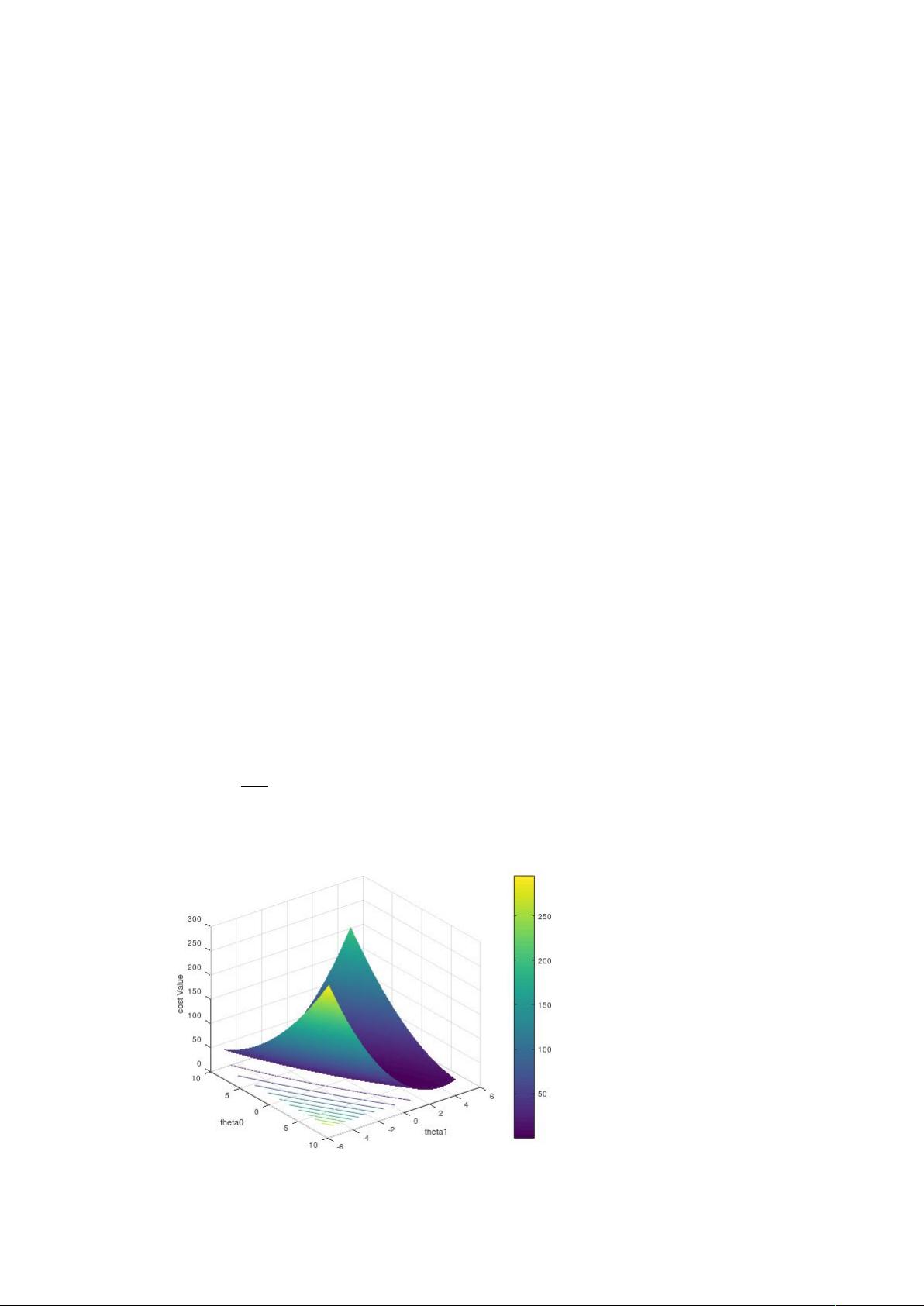
在"每天进步一点点《ML - 线性回归》"文档中，作者详细介绍了机器学习中的线性回归方法，这是监督学习的一个基础概念。作者强调，机器学习的目标是根据给定的输入实例（X）和期望输出（Y），通过训练一个模型（P），预测新的未知实例的输出。文档特别提到了监督学习与非监督学习的区别，前者如线性回归和分类，后者则是数据的自动聚类。 在文章的起始部分，作者提到他们的学习主要基于Andrew Ng的斯坦福大学录制的机器学习课程，并表示文章是个人学习的记录和分享，适合初学者阅读，同时也欢迎读者提出反馈以进行修正和更新。作者设定了一些约定，比如使用大写字母表示矩阵或向量，明确了实例矩阵X的维度和结构，以及参数向量θ的定义。 线性回归是文章的核心部分，其模式表示为H(θ)(X) = Xθ，这里的X是一个M*N的实例矩阵，θ是一个N*1的参数向量。每个实例的预测输出Y(i)可以通过将X(i)与θ相乘得到，形式上即Y(i) = (1, X(i)')(θ0, θ1, ..., θN)'，其中X(i)'是第i个实例特征向量的转置。 线性回归被定义为对连续数值的预测，它假设输出与输入特征之间存在线性关系。作者会通过大量的计算过程和图示来解释如何估计参数θ，例如最小二乘法或梯度下降等优化算法，以及评估模型性能的方法，如均方误差（Mean Squared Error, MSE）。 文档后续可能会探讨线性回归的适用场景、模型训练步骤、特征选择、正则化等关键知识点，这些都是理解和应用线性回归不可或缺的部分。这篇文章为初学者提供了一个从理论到实践理解线性回归的全面指南，是机器学习入门者学习这一核心概念的重要参考资料。