Mallat算法实现离散快速小波变换实验解析

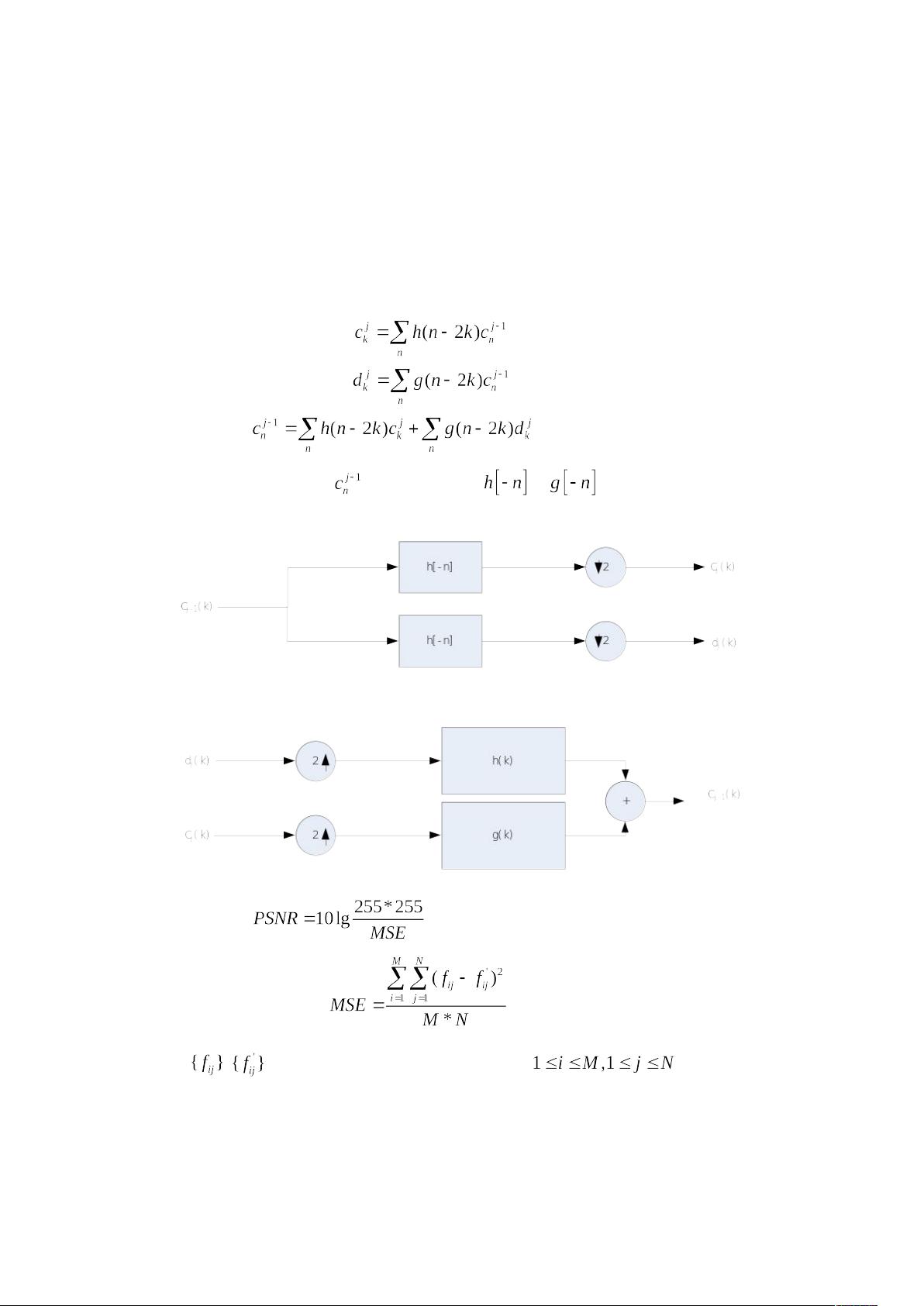
"小波变换 Mallat 算法用于二维图像的离散快速小波变换，通过编程实现，理解小波分解与合成，以及不同边界延拓方法的应用。" 小波变换是一种数学工具，它结合了频域和时域分析的优点，能够对信号或图像进行多尺度分析。Mallat算法是离散快速小波变换的一种实现，它通过滤波器和二进制抽样来高效地完成变换过程。 1. Mallat快速算法的核心是将图像或信号通过一组滤波器进行分解和重构。等式(1)和(2)代表了这个过程，其中[pic]和[pic]是滤波器的冲击响应，它们分别对应低频和高频信息。通过这些滤波器，图像被分解为不同频率成分，然后进行二进抽样，降低数据量的同时保留关键信息。在重构阶段，等式(3)描述了如何利用这些分解得到的系数来恢复原始图像。 2. 在二维小波变换中，原始图像[pic]通过小波变换可以得到低频系数[pic]和高频系数[pic]。重构时，这些系数与适当的滤波器进行卷积操作，以恢复图像的细节和结构。 3. 边界延拓是处理图像边缘问题的关键步骤，因为它影响到小波变换的精度。实验中采用了四种常见的边界延拓方法：零延拓、周期延拓、对称周期延拓和常数连续延拓。每种方法都有其优缺点，适用于不同的应用场景。实验中通过调用相应函数实现这些延拓方式。 4. 实验的编程思路是基于循环结构，分别计算出低频和高频部分的分解系数。程序首先通过填充零来确保滤波器长度与输入信号一致，然后通过循环计算下一级的分解系数。对于重构，使用了频域卷积的方法，即通过快速傅里叶变换(FFT)和点乘操作来代替常规的卷积运算，提高了计算效率。 5. 在MATLAB中实现这一算法，首先获取输入信号的长度，然后通过循环迭代计算低频分量[pic]和高频分量[pic]。最后，通过逆快速傅里叶变换(IFFT)和滤波器系数的频域乘法，实现了图像的重构。 总结来说，小波变换Mallat算法提供了一种有效的方法来分析和重构图像，通过编程实现这一算法，可以深入理解小波变换的基本原理和实际应用，为后续的信号处理和图像分析奠定基础。实验过程中涉及的编程技巧，如滤波器设计、边界处理和频域运算，都是在信号处理和计算机视觉领域中至关重要的技能。