堆排序详解：小根堆构建与代码实现

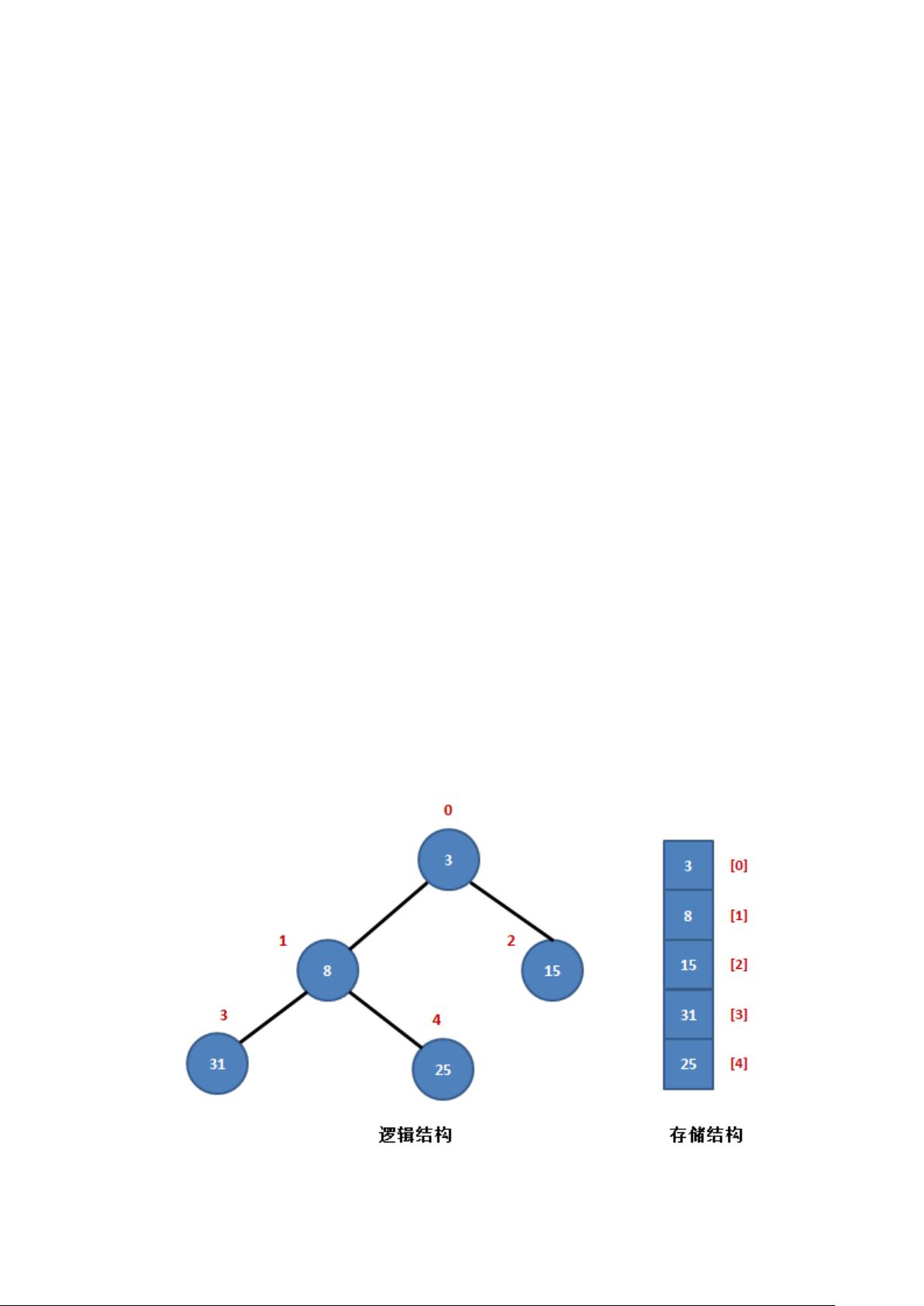
堆排序算法是一种高效的排序方法，它利用了堆数据结构的特点来进行操作。堆是一种特殊的完全二叉树，分为两种类型：小根堆和大根堆。小根堆的特点是每个节点的值都小于或等于其子节点的值，而大根堆则是每个节点的值大于或等于其子节点的值。堆排序的核心思想基于这两种堆的特性进行。 堆排序的主要步骤可以概括为两个关键操作： 1. **构建初始堆**： - 首先，将待排序的数组视为一个完全二叉树，然后根据堆的性质（小根堆或大根堆），逐层调整节点，确保每个父节点的值满足大于（小根堆）或小于（大根堆）其子节点的条件。 - 具体实现时，从最后一个非叶子节点（即最后一个内部节点，即 (n/2) - 1 级别）开始，自下而上地进行调整，这样保证了堆的正确性。 2. **交换和调整堆**： - 将堆顶（即最大值或最小值，取决于堆类型）与最后一个元素交换，然后删除最后一个元素（已排序）。 - 重新调整剩余元素为新的堆，保持堆的性质，然后重复此过程，直到整个数组只剩下一个元素，此时数组已经有序。 以Java为例，`HeapSort`类中的`heapify`函数用于维护堆的结构，`buildMaxHeap`函数则用于创建初始堆。完整的堆排序算法流程如下： - 输入无序数组，如 {1,3,4,5,2,6,9,7,8,0}。 - 创建初始堆，使得最大值位于堆顶。 - 交换堆顶元素（最大值）与末尾元素，输出最大值。 - 删除末尾元素，剩余元素重新调整为堆。 - 重复此过程，每次迭代减少一个元素，直到所有元素都有序。 通过这些步骤，堆排序实现了时间复杂度为O(nlogn)的排序，空间复杂度为O(1)，因为它不需要额外的存储空间。堆排序适用于对内存有限制但对排序速度有较高要求的场景。 总结起来，堆排序是一种基于比较的、高效的排序算法，通过构建和调整堆来达到排序的目的。理解堆的数据结构和堆排序的过程是掌握该算法的关键。