C语言动态规划：最短路径问题详解

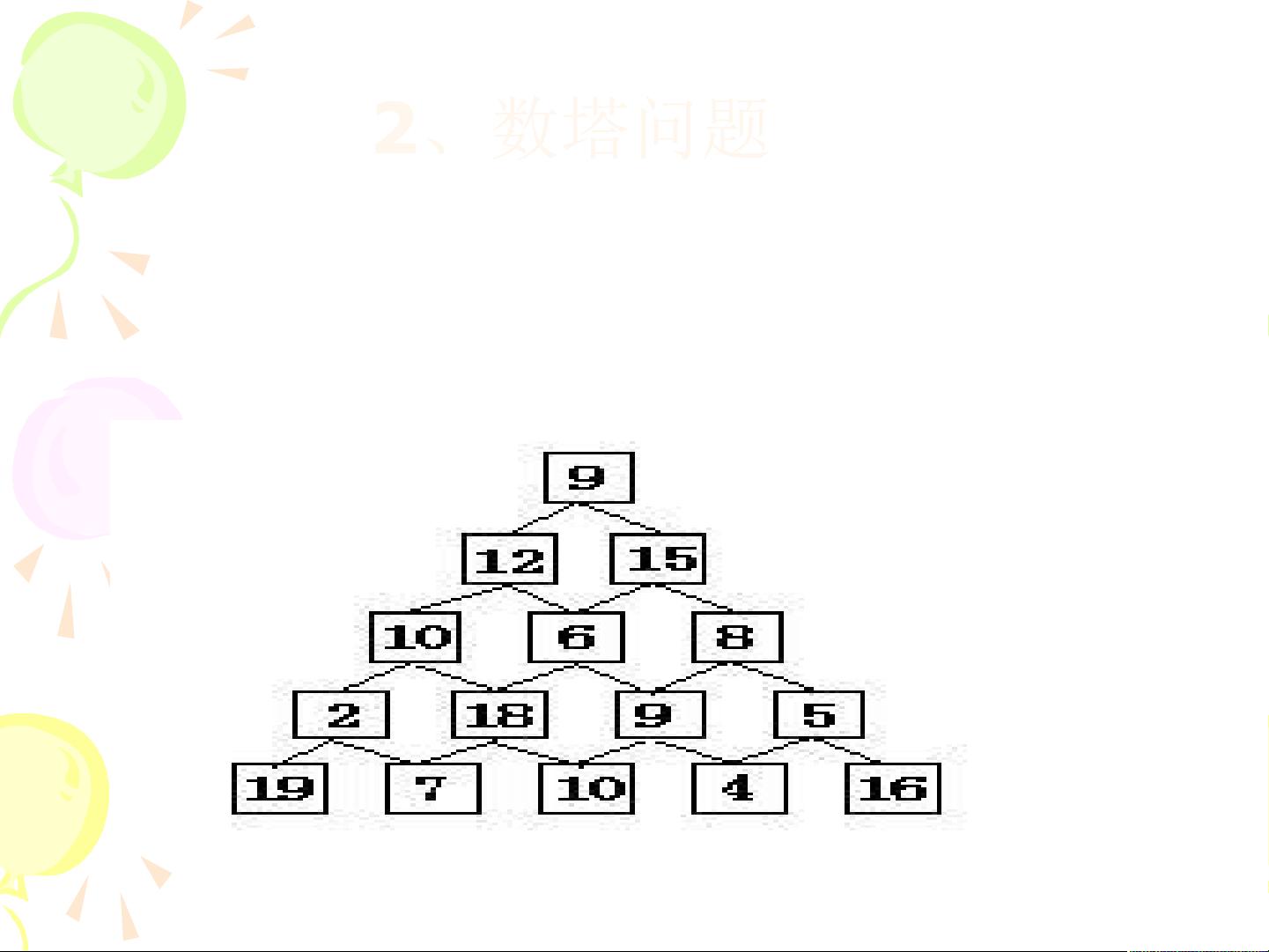
C语言动态规划是一种在编程中广泛应用的算法设计技术，它通过将复杂问题分解成更小的子问题并存储已解决结果来避免重复计算，从而提高效率。本资源主要聚焦于C语言中的动态规划应用，从第十章的内容来看，它涉及以下关键知识点： 1. **递推与递归的关系**：动态规划通过用递推的方式（自底向上解决问题）代替递归（自顶向下解决问题），减少了函数调用的次数，节省了时间和空间。这种方法特别适用于那些具有重叠子问题和最优子结构的问题。 2. **动态规划实例：最短路径问题** - 以城市交通网络为例，通过将问题划分为四个阶段（A到B，B到C，C到D，D到E），每个阶段都有可能选择不同的路径。动态规划的关键在于确定每个阶段的最佳决策，使得整个旅程费用最小。决策过程从目标状态E开始，逐步向前推进，每次选择当前阶段最短的路径作为子问题的解。 3. **策略与决策过程**：在最短路径问题中，策略是根据每个阶段到E的最省费用来选择决策路径。具体步骤包括： - 将目标分解为子问题，如从D到E，再到C，B，A。 - 从最终目标（E）开始，逆向计算每个阶段的最优解，即从后往前寻找最短路径。 - 每个阶段的决策是基于前一阶段的最优结果，形成一个决策序列，确保总路程最短。 4. **状态转移方程**：在C语言中实现动态规划时，通常会定义一个二维数组或表，用于存储子问题的解，以便后续使用。这个过程涉及到状态转移方程的设置，即根据已知的子问题解计算出更复杂问题的解。 5. **空间换时间的优势**：动态规划在处理大规模问题时，虽然会消耗额外的空间（存储子问题的解），但避免了重复计算，因此在时间效率上优于直接算法。这对于内存限制严格的场景尤其重要。 6. **C语言实现动态规划**：实际操作中，会使用C语言的数据结构（如数组、指针等）来存储和更新中间结果，并通过循环结构执行递推，最后返回整个路径的最优解。 C语言动态规划课程涵盖了理论概念、问题分析方法以及实际编程技巧，是计算机科学中解决复杂问题的重要工具。通过理解递推、子问题划分和状态转移，学生能够运用C语言有效地编写动态规划解决方案。