浮点数的内存存储：IEEE 754标准解析

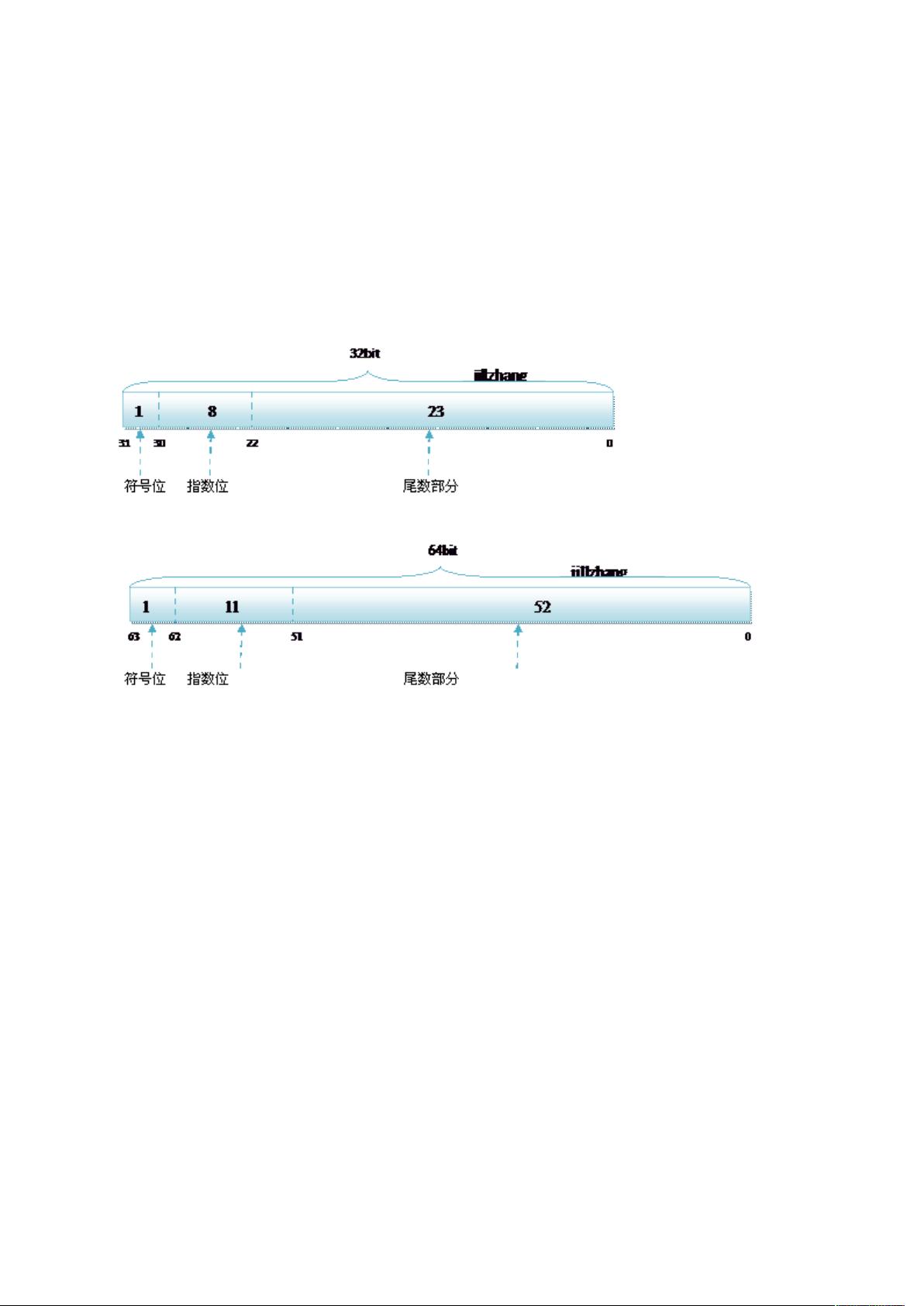
"浮点数在计算机内存中的存储遵循IEEE规范，包括单精度(float)和双精度(double)两种格式。float占用32位，double占用64位。这两种类型的存储结构均包含符号位、指数位和尾数部分。符号位表示数值的正负，指数位存储科学计数法的指数，尾数部分存储有效数字。对于float，有1位符号位，8位指数位和23位尾数；double则有1位符号位，11位指数位和52位尾数。由于尾数部分首位默认为1，因此实际精度比位数多一位。指数部分通过移位存储，加上偏移值（对于float是127，double可能是1023）来表示正负指数。例如，8.25在内存中存储为1.0001*2^3，120.5存储为1.1101101*2^6，经过转换后存储这些二进制表示。" 在计算机科学中，浮点数的存储是一个关键概念，因为它们被广泛用于各种计算，尤其是在科学计算和图形处理中。IEEE 754标准定义了如何在二进制中表示浮点数，以确保跨平台的一致性。单精度浮点数(float)按照R32.24格式存储，即32位中包含1位符号位，8位指数位和23位尾数。双精度浮点数(double)遵循R64.53格式，拥有1位符号位，11位指数位和52位尾数。 浮点数的存储过程首先涉及到将其转换为二进制科学计数法。例如，浮点数8.25转换为1.00001*2^3，120.5转换为1.1101101*2^6。在内存中，指数位使用移位存储法，这意味着指数值会加上一个偏移量（对于float是127，这是因为指数范围是-127到128，通过加127可以使其全部变为正数）。然后，当读取时，这个偏移量会被减去以恢复原始指数值。 尾数部分，也称为 significand 或 mantissa，通常不存储最前面的1，因为这是固定的。这增加了表示的精度，使得float可以精确到小数点后6位，而double可以达到15位。尾数部分的二进制形式用于存储数值的有效数字部分，对于float，实际精度为24位，因为第一位总是1，但不存储；对于double，实际精度为53位。 理解浮点数的内存存储对于优化代码性能、分析精度损失以及解决数值计算问题至关重要。例如，当进行高精度计算或需要节省内存时，可能需要选择使用double而不是float。另一方面，如果对速度有较高要求并且可以接受较低精度，float可能是更好的选择。了解这些内部工作原理可以帮助开发者更好地理解和处理浮点数相关的编程挑战。