栈的出栈序列与卡特兰数的动态规划和组合证明

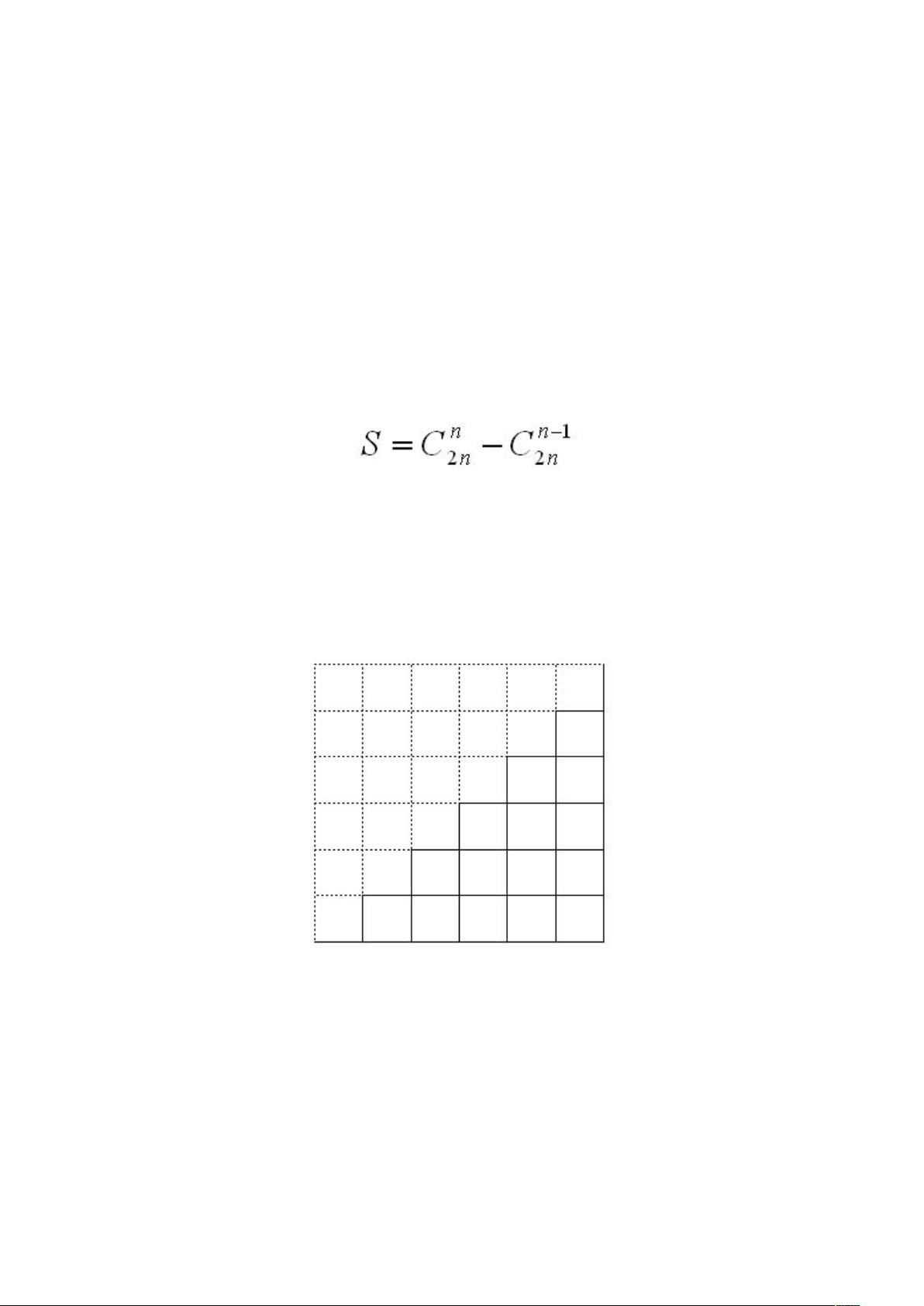
"出栈序列和卡特兰数" 出栈序列个数是组合数学中的一个有趣问题，它涉及到栈这种数据结构的操作以及卡特兰数的应用。卡特兰数，又称卡塔兰数，是一类在组合数学中频繁出现的数列，它在解决许多计数问题时起到关键作用。在本问题中，我们要找出给定n个元素的可能出栈序列的数量。 首先，我们可以直接模拟栈的操作来解决问题，但这在n较大时效率较低。为了优化，可以采用动态规划的方法。定义状态f[i,j]，表示栈内有i个元素，栈外还有j个元素未进栈。根据进栈和出栈两种操作，我们可以得到转移方程f[i,j]=f[i-1,j]+f[i+1,j-1]，这样避免了重复计算，提高了效率，但依然属于指数级的时间复杂度。 另一种更巧妙的方法是利用卡特兰数。我们可以将n次进栈和n次出栈的过程看作是在一个n×n的网格中，从左下角向右上角移动，每次只能向右或向上一步。由于出栈次数不能超过进栈次数，所以路径只能沿着实线行走。合法的路径数量就是我们需要的卡特兰数。 证明卡特兰数公式可以通过图形化的解释来完成。设想将不合法的路径（出栈次数多于进栈次数）反转，这样就会形成一个新的路径，它位于一个(n+1)×(n-1)的网格中。每条不合法的路径都与这个更大网格中的一条路径一一对应。通过这样的对应关系，我们得出不合法路径总数为C(2n, n-1)，而所有路径总数为C(2n, n)，两者的差值即为卡特兰数C(2n, n)，这也是n个元素的合法出栈序列数量。 此外，还可以从二进制数的角度理解这个问题。将进栈和出栈分别看作二进制数中的1和0，一个合法的出栈序列对应于一个2n位的二进制数，其中n个1代表进栈操作，n个0代表出栈操作。由于元素按1到n的顺序入栈，出栈序列的二进制形式中1的个数必须大于等于0的个数，因此总的出栈序列数等于满足条件的二进制数的个数，这也等于卡特兰数C(2n, n)。 出栈序列问题的解决方案可以通过动态规划、图形化证明和二进制数的计数原理，而这些问题的核心都涉及到卡特兰数。了解和掌握卡特兰数的计算及其应用，不仅有助于解决这类问题，也是深入理解组合数学和计算机科学中的计数问题的关键。