无超调最优Laplace逆变换：数值实现与矩阵指数分布

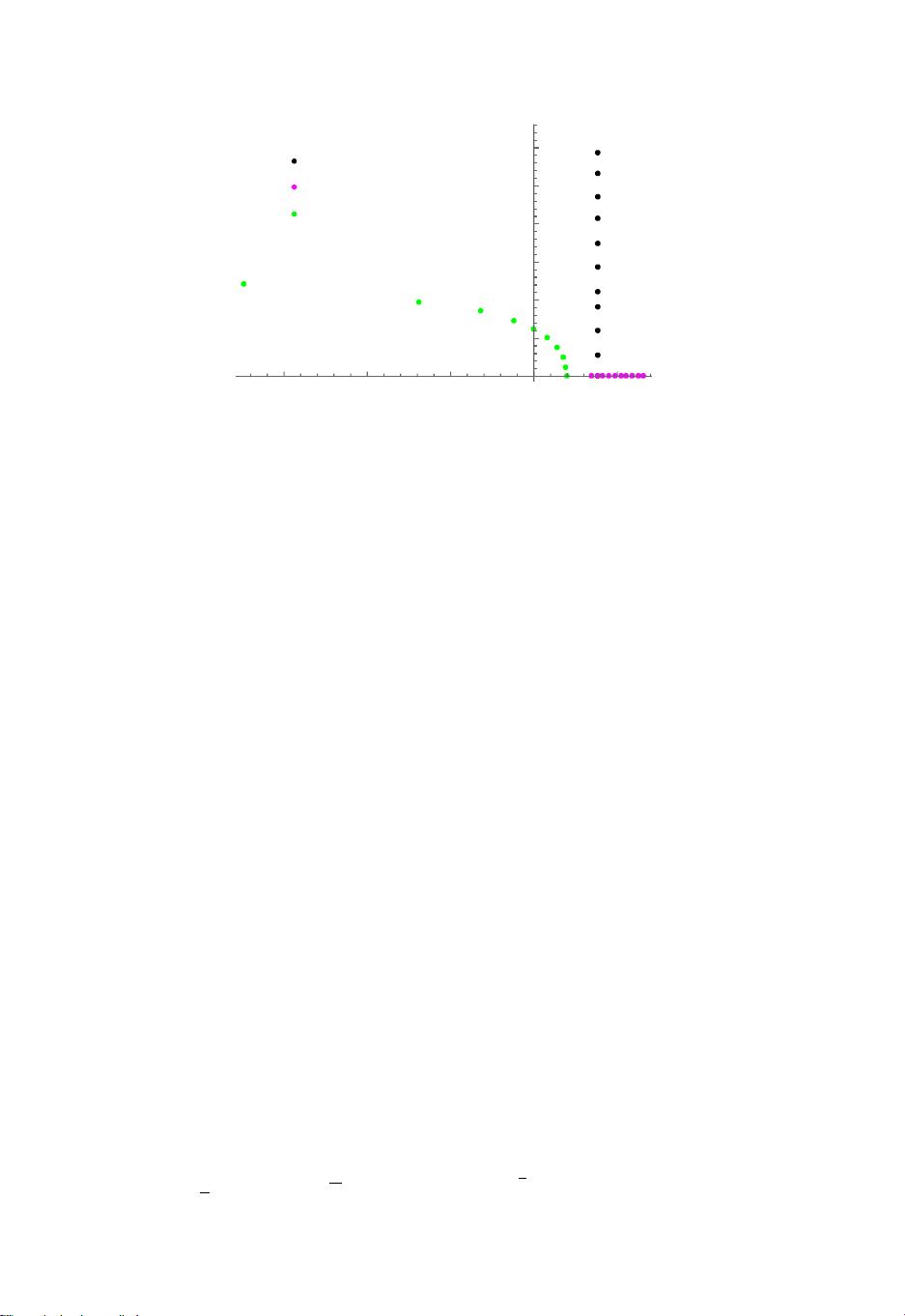
"该文提出了一种无超调的最优Laplace逆变换方法，主要应用于数值拉普拉斯逆变换，特别关注在随机模型中的应用，确保变换过程不会导致数值结果超出0到1的范围。文章由匈牙利的研究团队完成，并在理论计算机科学电子笔记上发表。该方法基于最小变差系数的矩阵指数（ME）分布，提供了一种避免正负超调的解决方案。关键词包括数值逆拉普拉斯变换、矩阵指数分布、超调和最小变异系数。文章还提及了数值逆变换方法的挑战，即正负过冲可能导致的数值误差，并指出已有大量相关方法但缺乏清晰的分类。" 本文主要探讨了在数值计算中处理Laplace逆变换时如何避免超调问题。在随机建模中，由于数值逆变换可能会产生正负过冲，导致结果不准确，这是需要解决的关键问题。作者提出的无超调方法基于矩阵指数分布，该分布具有最小变差系数，从而能更精确地进行逆变换。这种方法的优势在于能够确保变换后的数值始终保持在0和1之间，符合随机变量的概率性质。 Laplace逆变换在理论计算机科学中有广泛应用，特别是在涉及随机过程和概率分布的建模中。通过数值逆变换，可以将Laplace域的函数转换回时间域，这对理解和分析复杂的动态系统至关重要。然而，传统的数值逆变换方法常常伴随着正负超调的问题，即变换结果可能超出预期的范围，这对于模拟真实世界的随机事件是不允许的。 作者提到，尽管已有关于数值逆拉普拉斯变换的大量文献，但缺乏系统的分类和综合评估。这表明，尽管研究者们一直在寻找更有效的算法，但在方法的选择和比较方面仍然存在困难。该文为此提供了一个新的视角，即关注无超调这一特性，这可能会对未来的数值计算方法研究产生影响。 此外，文章也暗示了一个需求，即需要一个更清晰的方法分类框架，以便于研究人员更好地理解各种方法的优缺点，选择最适合特定问题的工具。这为未来的工作指明了一个可能的研究方向，即建立一个系统化的数值逆拉普拉斯变换方法分类体系，以促进领域的进步。