天津大学线性代数期末试卷：特征值、逆矩阵与二次型问题

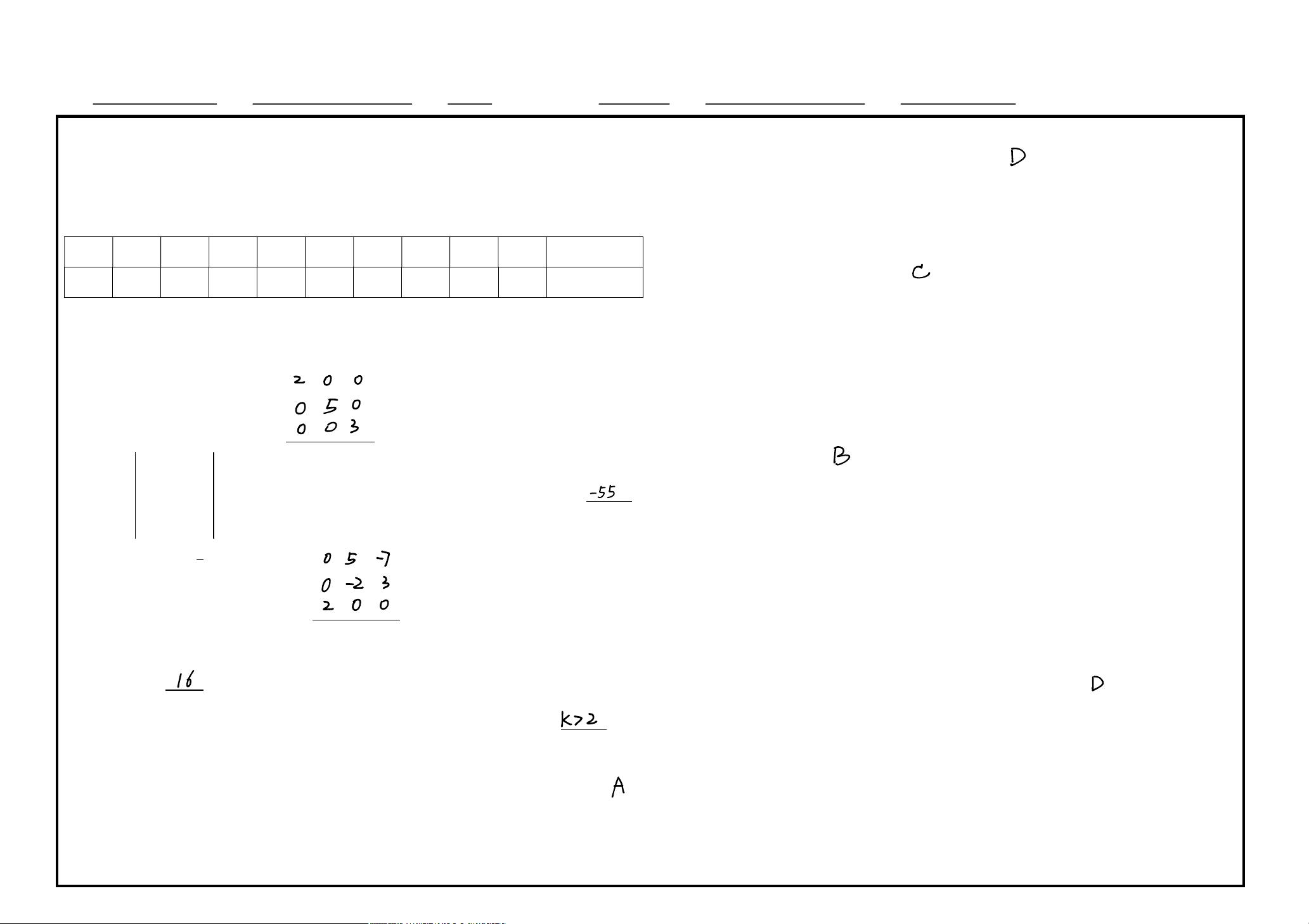
本资源是一份天津大学2016-2017学年第一学期期末考试的《线性代数》试卷A卷，涵盖了线性代数的基本概念和理论。以下是各部分知识点的详细解析： 1. **填空题** - 第一题要求计算矩阵S与A的特征向量对应的特征变换。根据题目，矩阵A的特征值为1, -1, 和0，对应的特征向量分别为X1, X2, X3。当对矩阵S进行特征变换时，即SAS，结果会与A的特征值相乘，因此填空部分应该是特征值的乘积，即SAS的结果为\[ \begin{bmatrix} 1 & 2 & 3 \\ 5 & 4 & 0 \\ 0 & 0 & 0 \end{bmatrix} \cdot A \cdot \begin{bmatrix} X_{11} & X_{12} & X_{13} \\ X_{21} & X_{22} & X_{23} \\ X_{31} & X_{32} & X_{33} \end{bmatrix} = \text{diag}(1 \cdot 1, -1 \cdot 2, 0 \cdot 3) \]。 - 第二题考查代数余子式的计算。行列式中元素\( a_{21} \)的代数余子式\( A_{21} \)是将行2和列1去掉后的子矩阵的行列式，根据给出的矩阵，计算后得到\( A_{21} = (1 \cdot 0 - 5 \cdot 3)(5 \cdot 2 - 1 \cdot 6) = -15 \cdot (-4) = 60 \)。 - 第三题考察矩阵的逆矩阵。对于矩阵A，其逆矩阵\( A^{-1} \)的求解涉及到行列式的计算和伴随矩阵的使用，由于具体数值没有给出，需要根据行列式公式计算或已知矩阵的逆矩阵形式来填写。 - 第四题是关于矩阵乘法的性质，如果矩阵\( A \)和\( B \)满足\( |8A| \neq 0 \)，那么矩阵\( B \)与\( A \)的秩相等，可以推断出\( |B| \neq 0 \)，因此矩阵B也是可逆的，所以填空部分应为\( |B| \neq 0 \)。 - 第五题涉及二次型的正定性判断。二次型\( f(x,y,z) = 5x^2 + 4xy + 2xz + kyz \)的正定性意味着矩阵\[ \begin{bmatrix} 5 & 2 & ky \\ 2 & 2 & 0 \\ ky & 0 & 2 \end{bmatrix} \]必须是对称且正定的，这意味着所有主子式的符号都为正，从而求得k的取值范围。 2. **选择题** - 第一题是关于特征值对线性方程组解的影响。因为特征值为1, -1, 0，根据线性代数原理，特征值为0对应特征向量构成的子空间使得方程组至少有一组非零解，所以答案是(A)有非零解。 - 第二题涉及矩阵相似性和合同性的判断。如果矩阵A和B相似，则它们有相同的特征值和行列式，但不一定是合同（即秩相同）。根据给出的矩阵，它们的秩不同，因此选项(C)相似且合同不成立，可能是(D)合同但不相似。 - 第三题是线性无关向量组的识别。向量组线性无关意味着没有任何一个向量可以表示为其他向量的线性组合。选项(A)中的第三个向量全为0，显然是其他两个向量的线性组合，因此线性相关，排除。其他选项没有提供具体的向量，但从一般规则判断，只有(B)中三个不同的向量组才可能线性无关，因为它们的分量都不相同。 总结，这份试卷主要考察了学生对线性代数基础概念如特征值、特征向量、行列式、逆矩阵、二次型正定性、矩阵运算及向量组线性相关性的理解和应用。解答这些问题需要扎实的理论基础和一定的计算能力。