计算机图形学基础变换矩阵总结-缩放、旋转、位移的重要性与应用

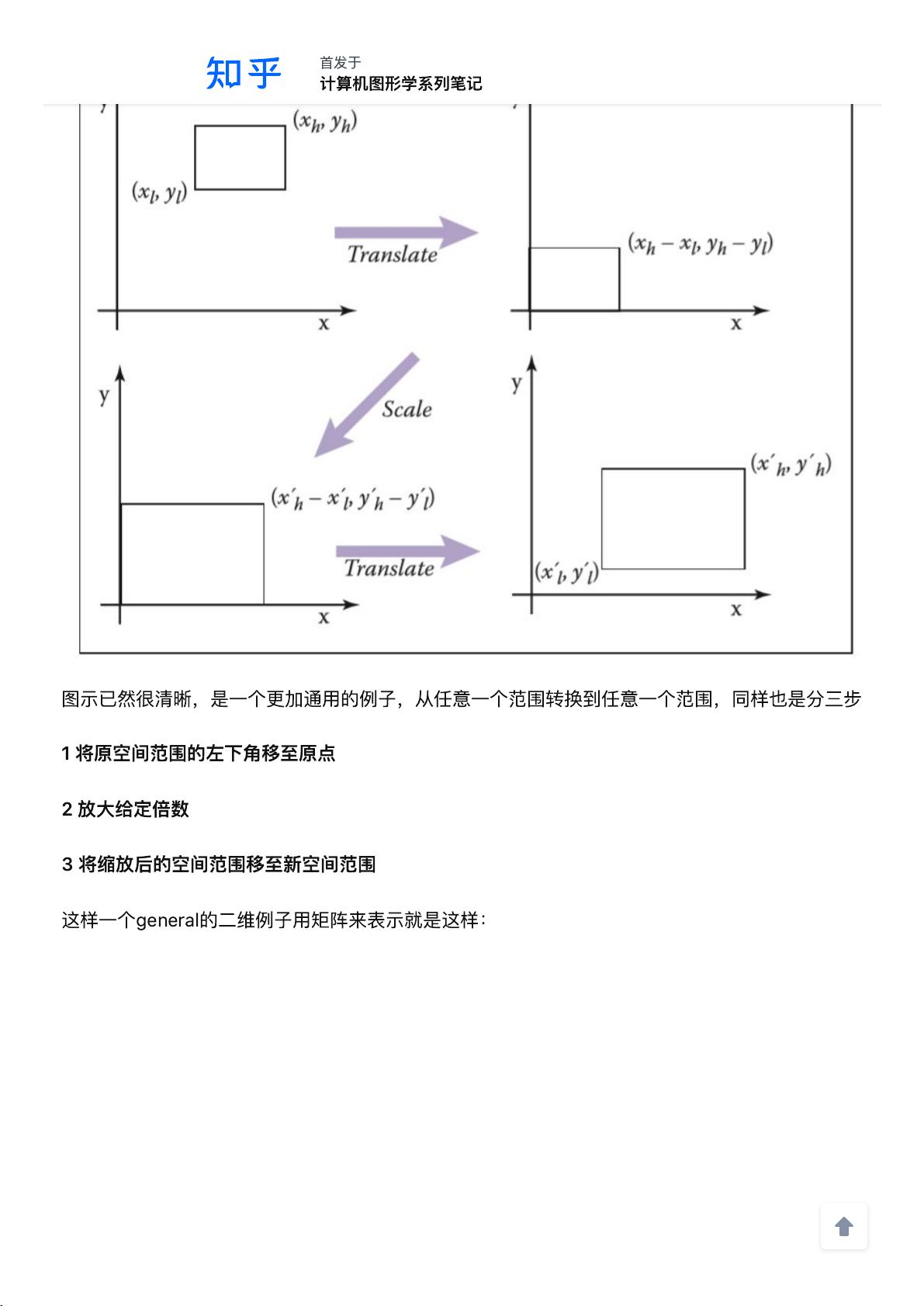
变换矩阵是计算机图形学中非常重要的工具，可以用于实现物体的缩放、旋转和位移。在投影变换中也有广泛的应用。本文将介绍一些简要的变换矩阵。 2D线性变换是指对向量进行线性变换，在图形学中常用的缩放变换是沿着坐标轴进行的变换。缩放变换的定义如下：对于一个二维向量(x, y)，经过缩放变换后的向量为(x', y')，其中： x' = sx * x y' = sy * y 其中，sx和sy分别表示在x轴和y轴上的缩放因子。例如，当sx和sy都为2时，缩放变换相当于将每个点沿着x轴和y轴同时扩大2倍。类似地，当sx和sy分别为0.5时，缩放变换相当于将每个点沿着x轴和y轴同时缩小一半。 旋转变换是将一个点绕着坐标原点进行旋转的变换。旋转变换的定义如下：对于一个二维向量(x, y)，经过旋转变换后的向量为(x', y')，其中： x' = cos(theta) * x - sin(theta) * y y' = sin(theta) * x + cos(theta) * y 其中，theta表示旋转的角度。例如，当theta为45度时，旋转变换相当于将每个点绕原点顺时针方向旋转45度。 位移变换是将一个点沿着坐标轴进行平移的变换。位移变换的定义如下：对于一个二维向量(x, y)，经过位移变换后的向量为(x', y')，其中： x' = x + tx y' = y + ty 其中，tx和ty分别表示在x轴和y轴上的平移距离。例如，当tx和ty都为1时，位移变换相当于将每个点在x轴和y轴方向上都移动1个单位。 综上所述，变换矩阵可以通过缩放因子、旋转角度和平移距离来描述不同类型的变换。通过乘上对应的变换矩阵，我们可以将二维或三维的向量进行缩放、旋转和位移的操作。这些基础变换矩阵在计算机图形学中起到了至关重要的作用，它们可以用于实现复杂的图形效果和动画效果。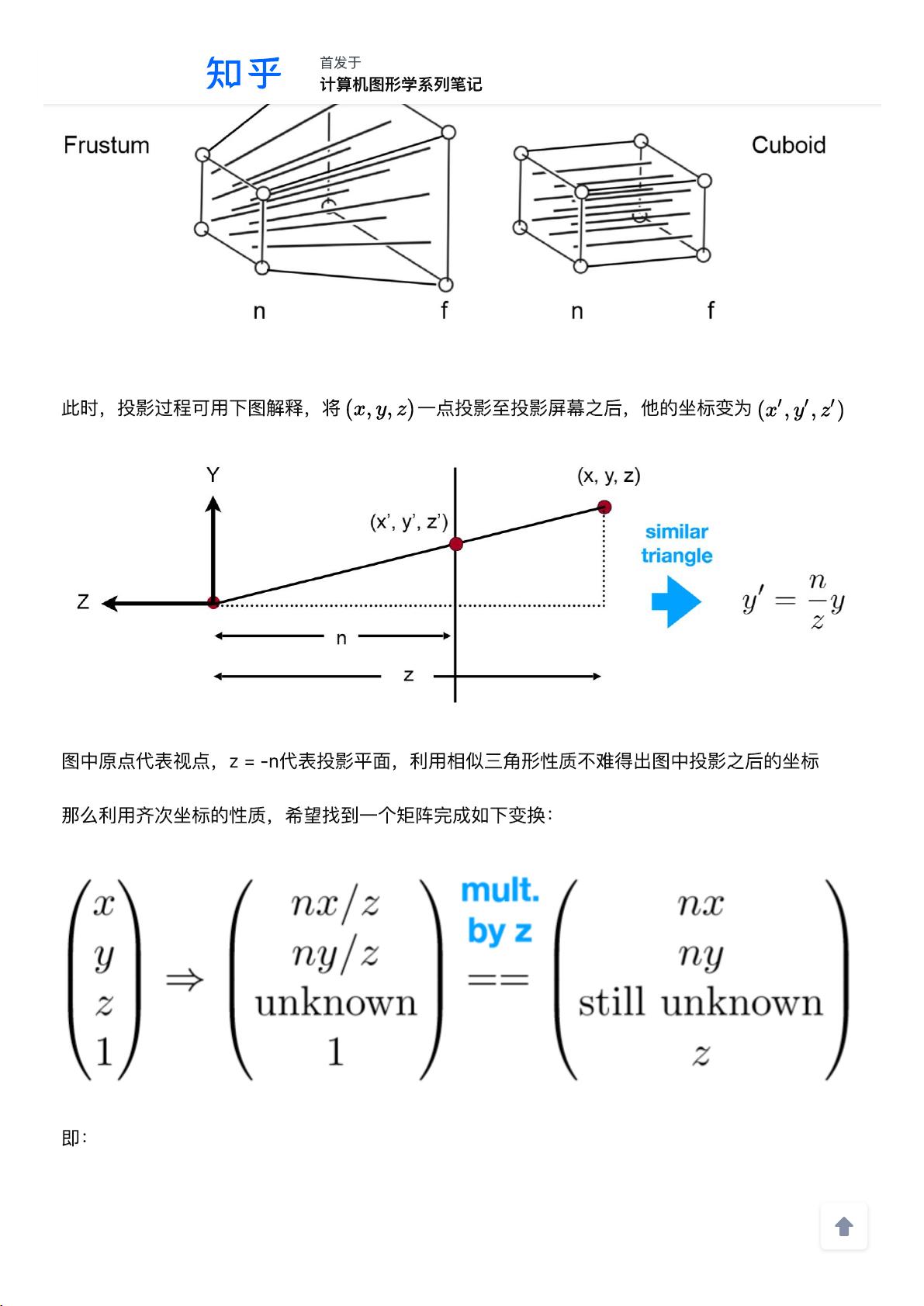 除了上述的基础变换矩阵外，还有投影变换矩阵等其他类型的变换矩阵在图形学中应用广泛。例如，在透视投影中，我们可以使用透视投影矩阵将三维场景投影到二维屏幕上，实现逼真的视觉效果。 总之，变换矩阵是计算机图形学中的重要工具，它们可以实现物体的缩放、旋转、位移和投影等操作。掌握变换矩阵的原理和应用，对于深入理解和应用计算机图形学是非常重要的。