理解一般线性模型GLMs：从最小二乘到最大似然估计

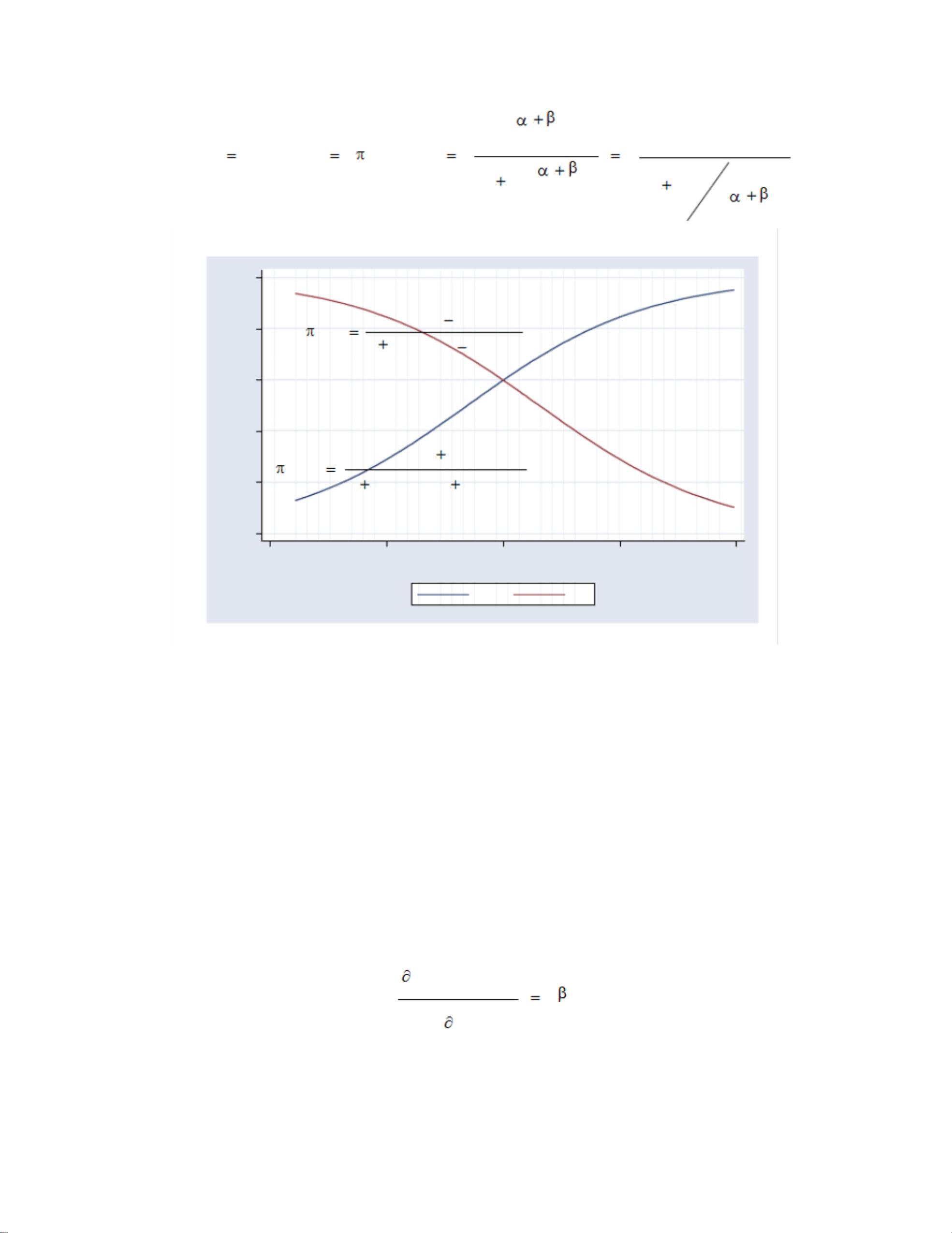
"类别数据分析实用.pdf - 介绍了一般线性模型GLMs的概念、要素以及在不同情况下的应用，如最小二乘法、logit模型和泊松回归模型，并提到了最大似然估计方法用于参数估计。" 在统计学和数据分析领域，一般线性模型（Generalized Linear Models, GLMs）是一种广泛使用的工具，它允许我们处理各种类型的数据分布，不仅限于正态分布。GLMs的核心包括三个关键要素： 1. 随机要素：定义了响应变量（因变量）Y的随机性，即Y所属的概率分布类型。例如，可以是正态分布、二项分布或泊松分布等。 2. 系统要素：这是一组解释变量（自变量），通常以线性组合形式出现，例如：β₀ + β₁X₁ + β₂X₂ + ... + βₖXₖ。这些变量用于构建预测模型。 3. 连结函数：连接随机要素和系统要素的非线性函数。它定义了期望值μ（E(Y)）与线性预测器之间的关系。不同的连结函数对应于不同类型的分布，如对数连结函数对应于泊松回归，对数it连结函数对应于逻辑斯谛回归。 GLMs的特殊形式包括： - 最小二乘法（Ordinary Least Squares, OLS）模型：适用于连续且符合正态分布的响应变量，连结函数为恒等函数，即g(μ) = μ。 - Logit模型：适用于二项分布的数据，如是/否、成功/失败的情况。连结函数为对数it函数，g(μ) = log[μ/(1-μ)]。 - 泊松回归模型：适用于计数数据，如事件发生的次数，其响应变量服从泊松分布。连结函数为对数函数，g(μ) = log(μ)。 除了这些，GLMs还可以应用于列联表分析中的Loglinear模型，它是泊松回归的一个特例。 参数估计通常采用最大似然估计（Maximum Likelihood Estimation, MLE）方法。该方法寻找一组参数值，使得给定数据出现的概率最大。首先，定义一个描述参数的似然函数，然后找到使这个函数值最大的参数值。以二项分布为例，MLE可以用来估计在一系列独立试验中观察到特定结果的概率。 GLMs提供了一个框架，可以整合并分析连续和离散变量的各种统计模型，而最大似然估计则是确定模型参数的有效手段。在实际数据分析工作中，理解并熟练运用这些概念和技术对于正确建模和解释数据至关重要。