Python概率分布与可视化全解析

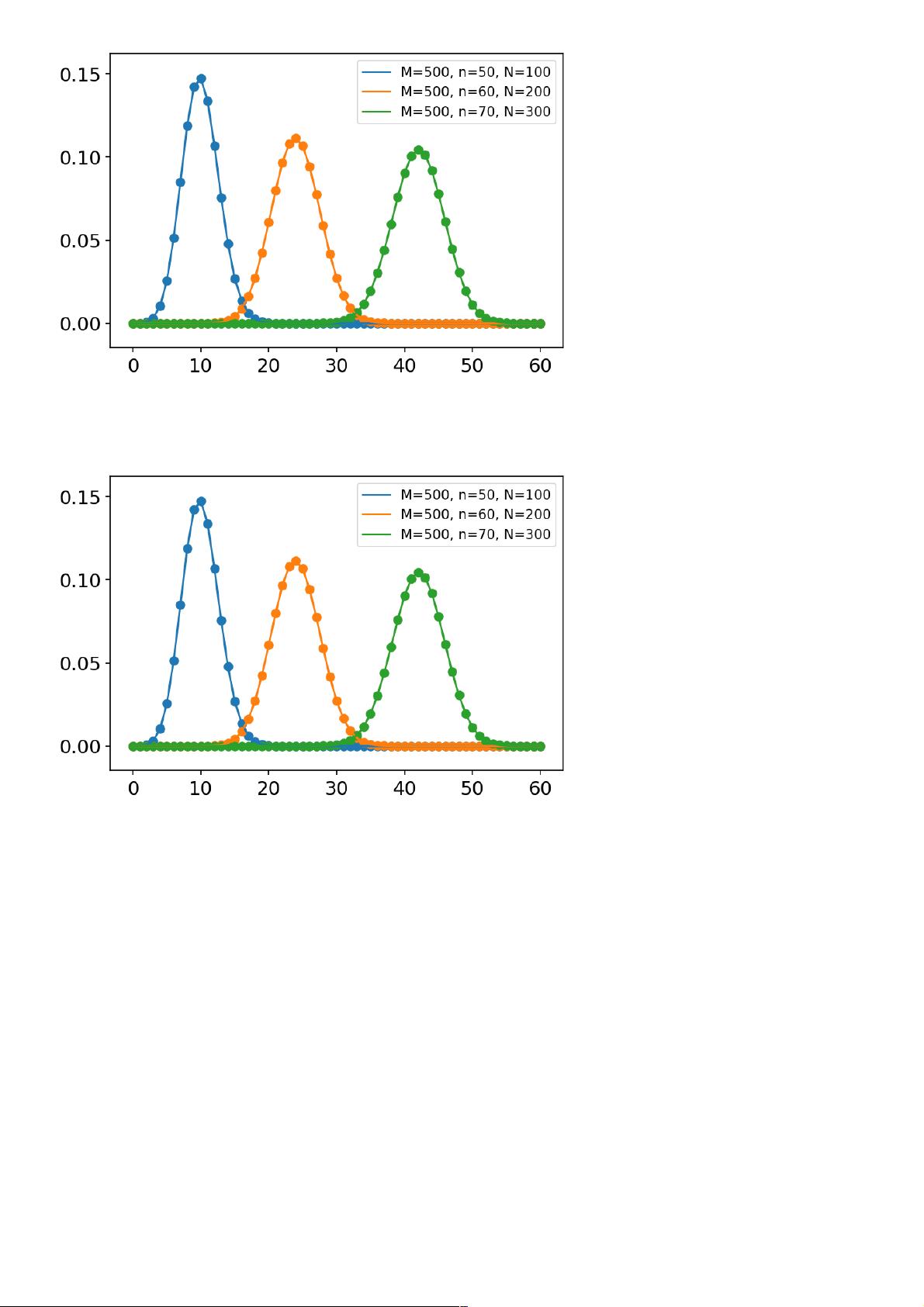
本文主要介绍了Python中用于生成和可视化各种概率分布的方法，涵盖了广泛的概率分布类型，包括贝塔分布、二项分布、卡方分布、狄利克雷分布、指数分布、F分布、伽玛分布、几何分布、耿贝尔分布、超几何分布、拉普拉斯分布、逻辑斯谛分布、正态分布、对数正态分布、对数分布、多项分布、多元正态分布、负二项分布、非中心卡方分布、非中心F分布、帕累托分布、泊松分布、幂律分布、瑞利分布、柯西分布、标准指数分布、标准伽马分布、标准正态分布、学生t分布、三角形分布、均匀分布、冯·米塞斯分布、逆高斯分布、韦伯分布和齐夫分布。文章还提到了相关的统计术语，如概率密度函数(pdf)、累积分布函数(cdf)、百分点函数(ppf)和概率质量函数(pmf)，并展示了如何使用numpy和scipy库来生成随机数和绘制分布图形。 在Python中，可以使用`numpy.random.Generator`类来生成随机数。例如，`integers`函数可用于生成指定范围内的整数。例如，`rng.integers(low=0, high=10, size=10)`将生成10个介于0到10（不包括10）的随机整数，而`endpoint=True`会将10包含在内。此外，通过设置`size`参数可以生成特定形状的数组。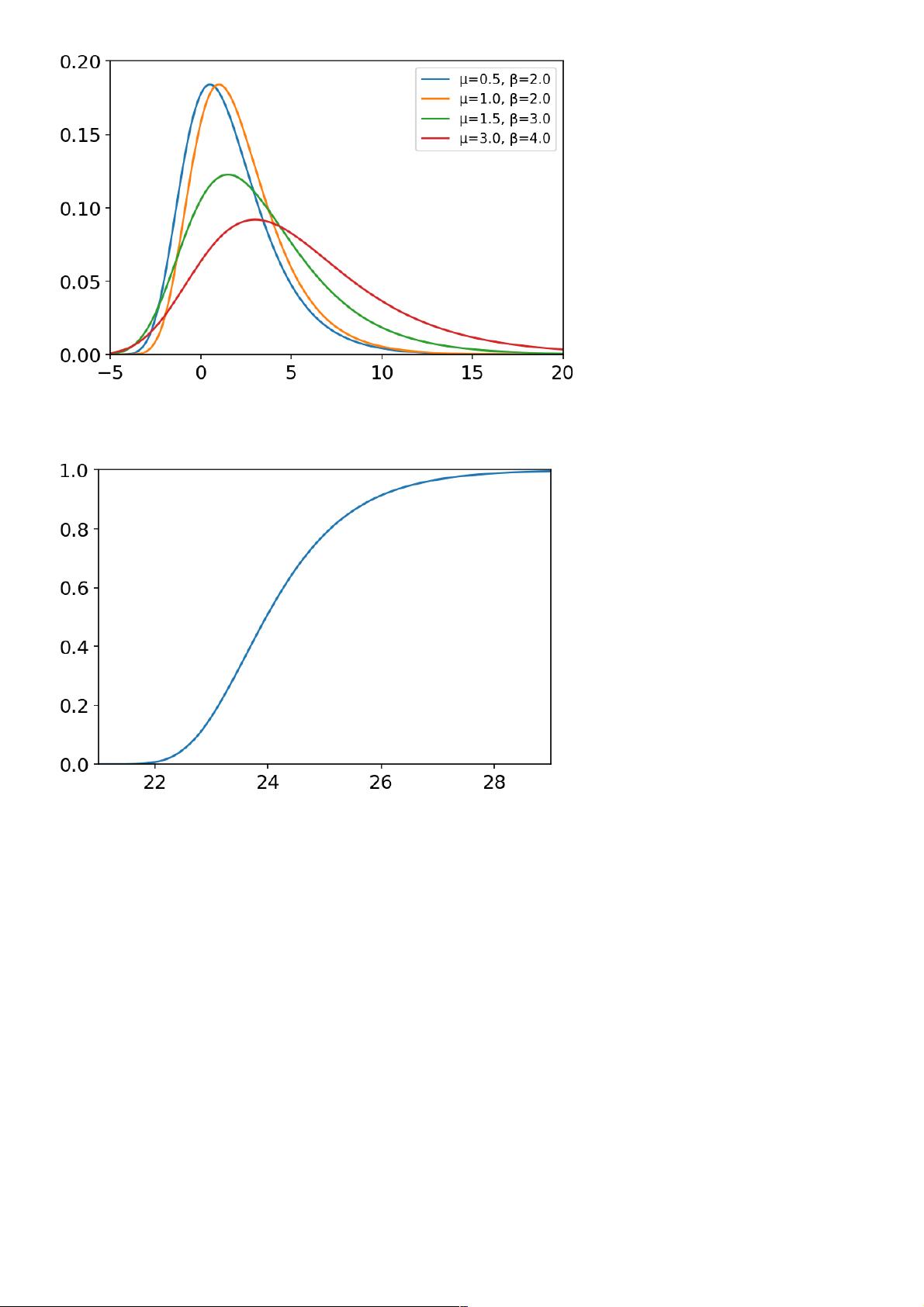 对于连续分布，如正态分布，可以使用`numpy.random.Generator.normal`方法生成样本。正态分布有多种函数，包括计算概率密度、累积分布、百分点等。例如，`stats.norm.pdf(x, mean, std)`计算x处的正态分布概率密度，其中mean是均值，std是标准差。 在进行可视化时，可以借助`matplotlib.pyplot`库绘制分布曲线。`plt.hist`函数可以用来绘制直方图，而`plt.plot`可以绘制连续分布的曲线。`plt.show()`用于显示图形。 为了更深入地理解这些分布，可以使用类似以下的代码绘制分布图： ```python mu, sigma = 0, 1 # 均值和标准差 s = np.random.normal(mu, sigma, 1000) plt.hist(s, bins=30, density=True, alpha=0.6, color='g') x = np.linspace(-3, 3, 100) p = stats.norm.pdf(x, mu, sigma) plt.plot(x, p, 'k', linewidth=2) plt.title('正态分布示例') plt.show() ``` 这篇文章提供了一个全面的指南，帮助读者了解如何在Python中生成和可视化各种概率分布，对于数据分析、机器学习和统计建模等领域非常有用。通过学习这些分布和它们的特性，可以更好地理解和模拟现实世界中的随机现象。