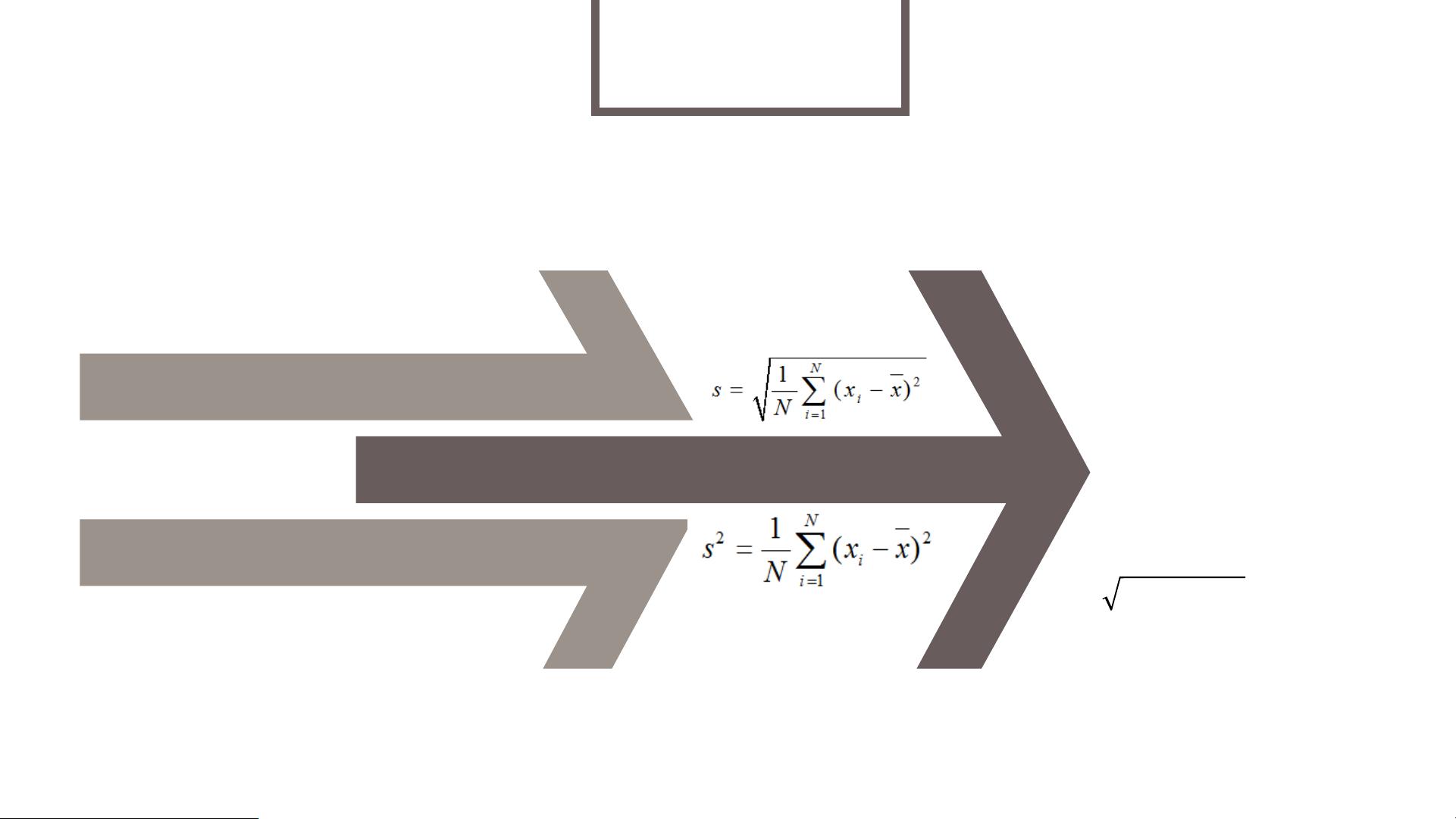空间数据分析:正态误差与描述性统计
需积分: 0 85 浏览量
更新于2024-06-30
收藏 3.76MB PDF 举报
本章节主要探讨了空间数据分析中的经典统计学基础,特别是描述性统计部分。首先,作者引入了正态误差理论,这是在最小二乘法基础上的重要补充,它强调了误差分布的正态特性,这一观点由高斯在1809年提出的元误差学说逐渐确立。海根在1837年的贡献在于处理了数据与正态分布拟合不理想的情况。
描述性统计是统计分析的基础,它通过制表、分类、图形和计算来概括数据特征。其中核心概念包括:
1. **均值**:是最常用的集中趋势度量,计算所有数值的算术平均,既包括简单的算术平均,也包括加权算术平均,后者考虑了数据中每个数值的重要性。
2. **中位数**:将数据分为两半的数值,对于非对称分布,中位数提供了不同于均值的另一个集中趋势指标。
3. **众数**:出现频率最高的数值,常用于描述数据的集中趋势,尤其在存在多个峰值的情况下。
4. **极差、四分距、百分位距**:衡量数据的离散程度,分别表示最大值与最小值之差、数据分布的中间40%的间距和将数据分为100份后各部分的宽度。
5. **平均偏差、标准差和方差**:衡量数据分散程度,标准差是方差的平方根,方差是各个数值与均值之间差异的平方的平均。
6. **变异系数**:标准差与均值的比例,用于比较不同数据集的分散程度,不受量纲影响。
7. **偏度**:数据分布的不对称程度,正值表示右偏,负值表示左偏,零则表示对称。
8. **峰度**:数据分布顶部尖锐程度的测量,大数值出现的频率,高峰度可能表示尖顶分布,低峰度可能表示平顶或双峰分布。
此外,还介绍了中心矩的概念,特别是1阶到4阶中心矩,它们分别对应期望、方差、偏度和峰度,这些都是描述数据分布形状的关键参数。
描述性统计部分着重讨论了均值、几何平均和调和平均的区别与联系。调和平均对于极端值敏感,并且在某些情况下(如数据中有0或者存在开口组)计算不稳定。而几何平均在等比关系的数据集中有应用,但它同样受极端值影响,且不能应用于含有0的数据。三个平均值的关系被总结为:调和平均(𝐻)小于等于几何平均(𝐺)小于等于算术平均(𝑿)。
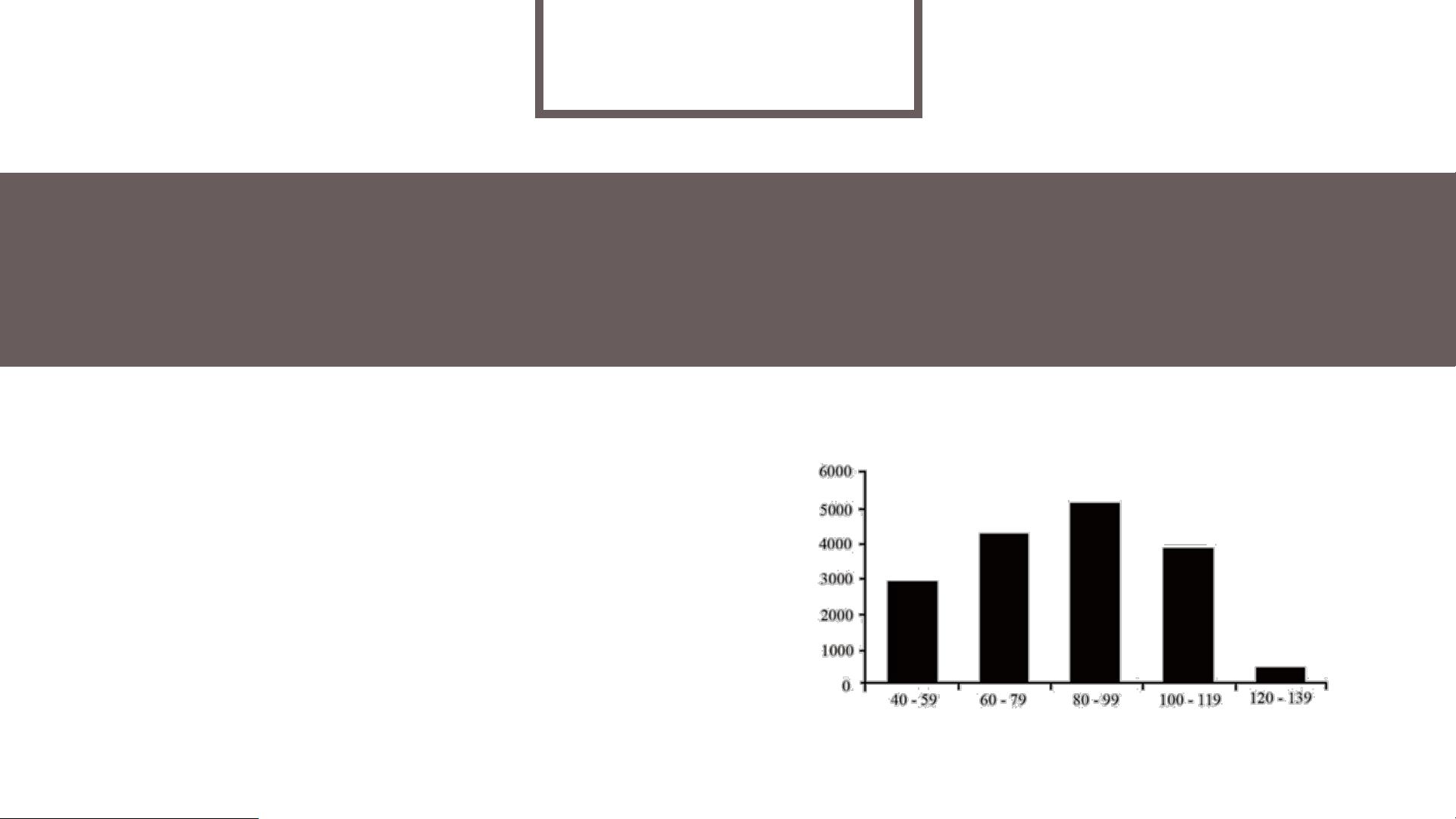
在实际案例中,如给出的12个区域物种数的分析,描述性统计可以帮助我们理解这些数据的集中趋势、离散程度以及整体分布情况,以便进行后续的数据分析和决策。
2020-04-22 上传
2022-08-04 上传
2022-08-03 上传
2022-08-03 上传
2011-03-25 上传
2011-03-25 上传
2011-03-25 上传
2011-03-25 上传
忧伤的石一
- 粉丝: 31
- 资源: 332
最新资源
- easymc:easymc.io的API,该站点允许您使用令牌登录Minecraft帐户
- thread-stream:一种将数据发送到Node.js辅助线程的流传输方式
- lab2Zad5
- Krumo-开源
- Megasena-crx插件
- chengfakoujue,c语言采蘑菇源码,c语言项目
- 独立按键_单片机C语言实例(纯C语言源代码).zip
- s9:基于 Svelte 的前端业务框架
- smartsoft:适用于任何角度,嵌套,离子项目的多种工具
- cofcod
- Notes_About_CL:对比学习笔记
- 安卓一个木函v7.9.8.8 多功能工具箱.txt打包整理.zip
- SCATTERSHAPE:将 SCATTER 中的补丁变成形状。-matlab开发
- burger_war_autotest:burger_war_autotest
- MatrixLiteLib,c语言源码中文版,c语言项目
- todo-code-along