谱聚类算法详解：Matlab 实现的图像分割教程

本文主要介绍了【图像分割】中基于谱聚类算法的Matlab源码实现。首先，我们从谱聚类的一般概念开始，强调了谱聚类作为一种新兴且受欢迎的聚类方法，尤其是在处理复杂数据集时，它相较于传统聚类算法如K-Means具有更好的聚类效果。谱聚类的核心思想在于利用样本数据构成的图论模型，通过计算拉普拉斯矩阵的特征向量来进行数据降维和聚类。 **1. 谱聚类的基本原理** - **谱方阵**：作为线性算子的特征值集合，谱半径指的是拉普拉斯矩阵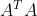的最大特征值，对于谱聚类算法至关重要。 - **谱聚类流程**：首先，构建样本点之间的相似度或距离关系，形成图的邻接矩阵或 affinity matrix。然后，计算拉普拉斯矩阵，它是邻接矩阵与度矩阵之差，用于捕获数据内在的结构信息。接着，对拉普拉斯矩阵进行特征值分解，选择对应的特征向量作为降维后的表示，这些向量对应的是数据在低维空间中的坐标。 **2. 聚类过程简述** - 输入：n个样本点构成的矩阵X，每个点表示为一个特征向量。 - **核心步骤**： - **构建图**：根据样本点间的相似度构建拉普拉斯矩阵L，通常用加权邻接矩阵或核函数计算点间关系。 - **特征向量**：求解L的特征值问题，得到特征向量，这些向量反映了数据在图上的局部连通性。 - **降维**：选择部分特征向量作为新的低维表示，这些向量可以用来执行后续的聚类任务，如KMeans。 - **优势**：谱聚类避免了K-Means对初始聚类中心敏感的问题，能够自动发现数据的自然聚类结构。 **3. 实现要点** - Matlab源码中可能涉及矩阵操作、特征值分解（如eig函数）、以及聚类算法的调用，比如用KMeans对低维表示进行聚类。 **4. 跨学科应用** - 掌握谱聚类有助于理解和掌握矩阵分析、图论、降维（如主成分分析PCA）等高级数学概念。 综上，这篇文档提供了实现图像分割的谱聚类算法的详细步骤，并通过Matlab源码的形式展示如何运用图论工具对高维数据进行降维和聚类，适合对谱聚类理论和实践感兴趣的读者深入学习。