解析机器人避障问题：最短路径与最短时间研究【建模集训】

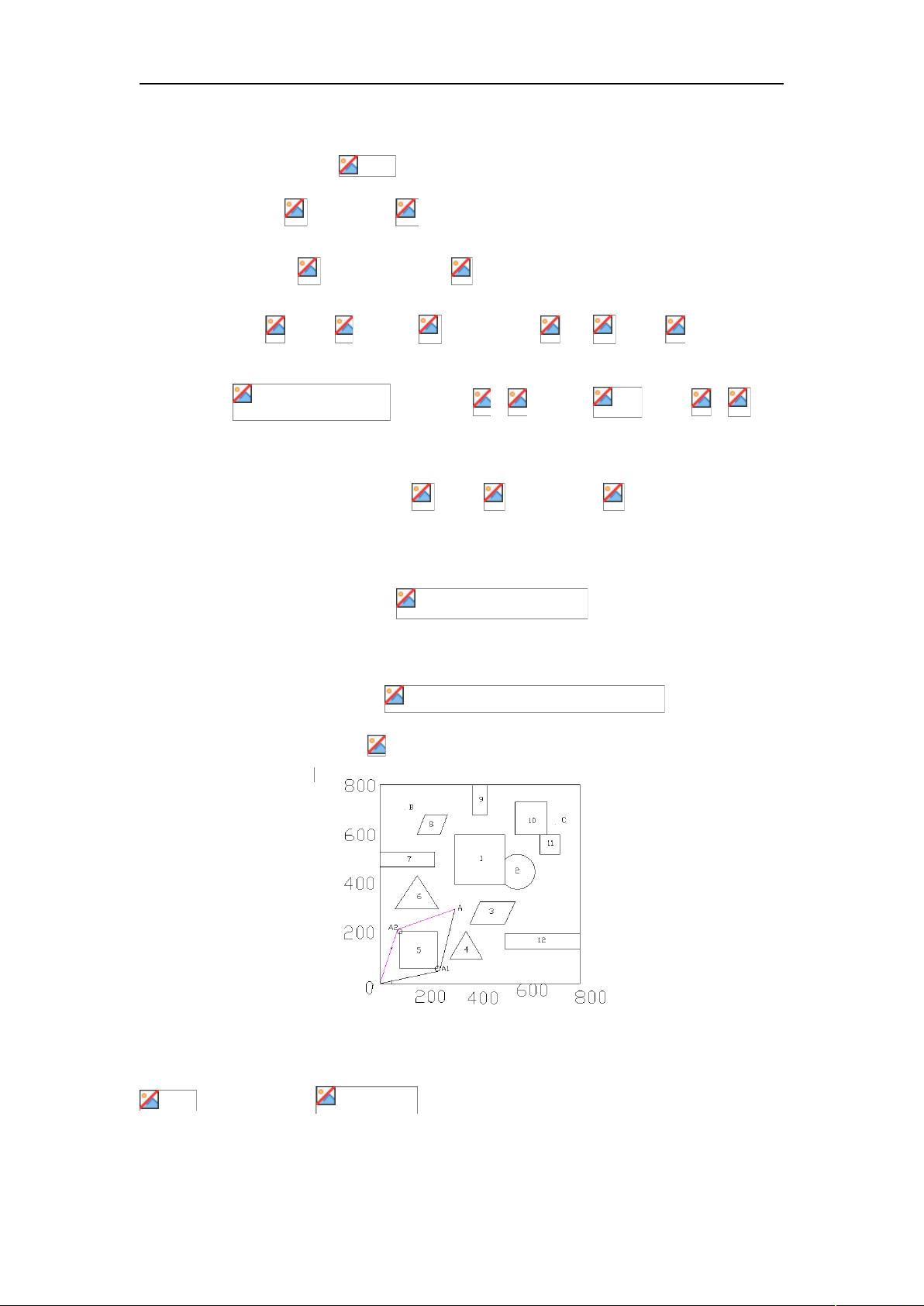
本文对2012年全国大学生数学建模竞赛D题机器人避障问题进行了全面的分析和建模研究。首先针对机器人避障问题，提出了最短路径和最短时间两个不同的问题，分别进行了理论分析和建模。在最短路径问题中，通过对Dijkstra算法的应用和几何模型的建立，成功地设计了机器人避障最短路径的模型，并对其进行了证明和分析。同时，针对最短时间路径问题，本文建立了非线性规划模型，有效地解决了转弯半径、圆弧圆心位置和行走时间等问题。通过对12个不同形状的静态障碍物的数学描述和模型建立，为机器人在800×800平面正方形区域内寻找安全高效的行走路径提供了重要的理论支持。 随着科学技术的不断进步，机器人在各个领域的应用越来越广泛，因此如何使机器人在工作区域内绕过各种障碍物，到达指定的目的地成为了一个重要且具有挑战性的问题。本文以2012年全国大学生数学建模竞赛D题“机器人避障问题”为例，对此问题进行了深入的研究和分析。 在研究中，本文首先提出了机器人避障问题中的两个不同的子问题，即最短路径问题和最短时间问题。针对最短路径问题，本文运用了Dijkstra算法，并建立了机器人避障最短路径的几何模型。通过理论分析和证明，成功地设计出了有效的路径规划模型，并对其进行了具体的优化和改进。同时，在最短时间路径问题中，本文建立了非线性规划模型，有效地解决了转弯半径、圆弧圆心位置和行走时间等关键问题。 另外，本文还对12个不同形状的静态障碍物进行了数学描述，并建立了相应的模型，为机器人在800×800平面正方形区域内寻找安全高效的行走路径提供了理论支持。通过对障碍物的特性进行具体的分析和建模，进一步完善了机器人的避障路径规划模型。 综上所述，本文通过对2012年全国大学生数学建模竞赛D题机器人避障问题的深入研究和分析，成功地建立了机器人避障最短路径和最短时间的数学模型，并对其进行了详细的理论分析和优化。通过本文的研究成果，不仅在理论上为机器人避障问题的解决提供了重要的参考和指导，也为机器人在实际工作中的路径规划和避障提供了重要的理论支持。希望本文的研究成果能够为相关领域的研究和实践工作提供有益的参考和借鉴。