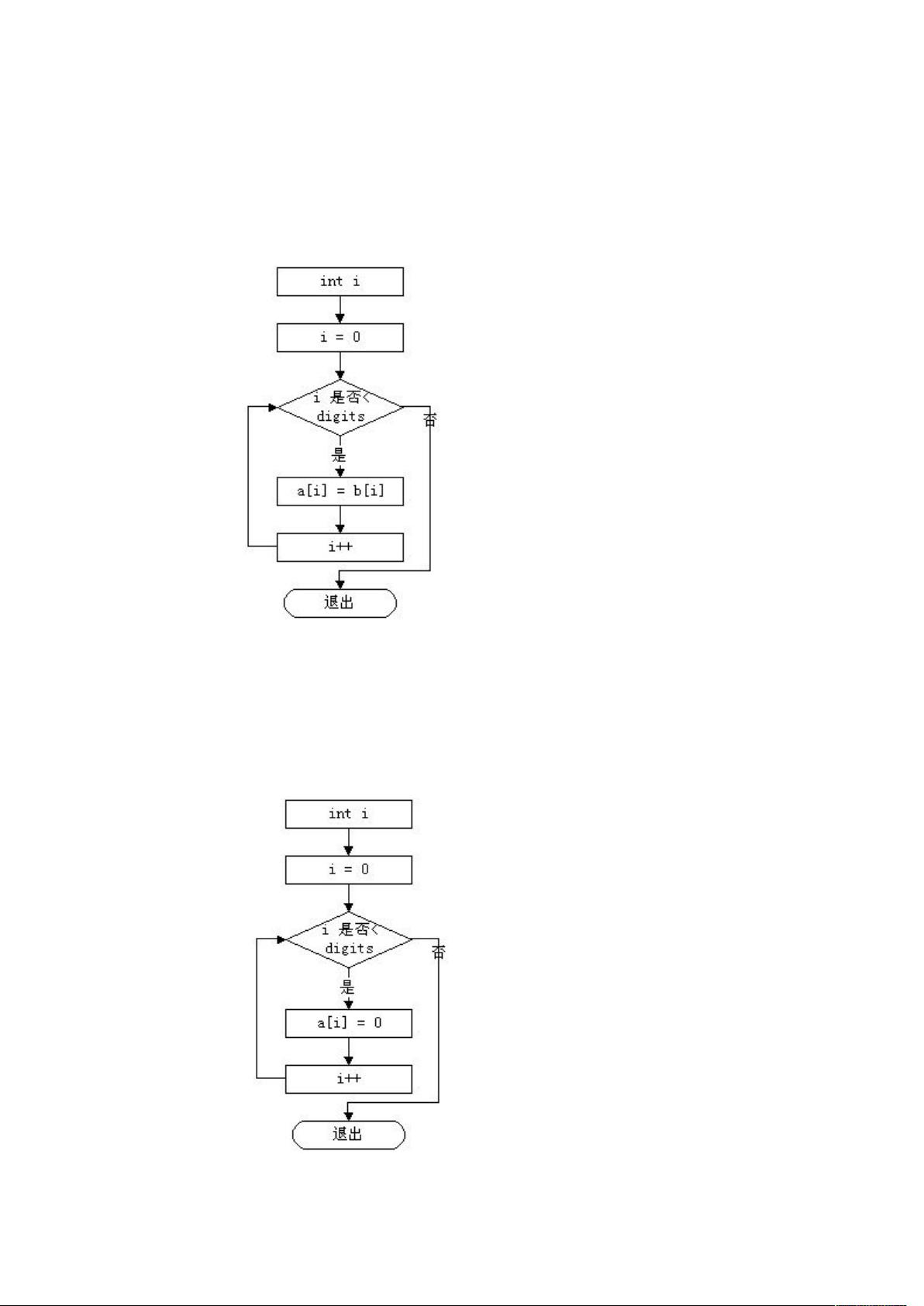
RSA加密算法详解及流程图

"RSA算法流程图ZL031125.doc" RSA算法是一种非对称加密算法，由Ron Rivest、Adi Shamir和Leonard Adleman在1977年提出，广泛应用于网络安全领域，如数字签名、数据加密等。其安全性基于大整数因子分解的困难性。 在RSA算法中，主要包括以下几个关键步骤： 1. **选择素数**：首先，选取两个足够大的素数p和q。这两个素数必须保密，因为它们是生成密钥对的基础。 2. **计算n**：将选取的素数p和q相乘得到n = p * q，n是公钥和私钥的模数，也是一个大整数。 3. **计算欧拉函数φ(n)**：φ(n) = (p - 1) * (q - 1)，欧拉函数在RSA中用于确定密钥的可选范围。 4. **选择加密指数e**：选取一个与φ(n)互质的整数e作为加密密钥，通常选择一个较小的素数，如65537，以便提高加密效率。 5. **计算解密指数d**：找到e关于φ(n)的乘法逆元d，即满足条件e * d ≡ 1 (mod φ(n))。这一步通常通过扩展欧几里得算法来完成。 6. **计算其他辅助值**：对于私钥，需要计算p和q的指数dP = d mod (p-1)、dQ = d mod (q-1)以及q的乘法逆元qInv，这些值用于提高解密过程的效率，尤其是当n非常大时。 7. **公钥和私钥生成**：公钥包含n和e，私钥包含n、d、p、q、dP、dQ和qInv。公钥可以公开，而私钥必须严格保密。 在文档资料中，可以看到`R_RSA_PUBLIC_KEY`结构体表示公钥，包括了模数n、公钥指数e。而`R_RSA_PRIVATE_KEY`结构体表示私钥，除了n和e之外，还包括了私钥指数d、素数p和q及其相关的辅助值。 代码中定义的数据类型如`UINT4`和`UINT2`用于存储整数，`NN_DIGIT`和`NN_HALF_DIGIT`定义了位宽，`NN_DIGIT_BITS`和`NN_HALF_DIGIT_BITS`分别设为32和16位，`MAX_NN_DIGIT_LEN`用于计算大整数的字节数。 宏定义`NN_DIGIT_LEN`计算出一个NN_DIGIT占用的字节数，而`MAX_RSA_MODULUS_LEN`和`MAX_RSA_PRIME_LEN`则限制了模数n和素数的最大长度。 RSA算法的工作原理是：明文m通过公钥(e, n)加密成密文c，计算公式为c = m^e mod n；密文c通过私钥(d, n)解密回明文m，计算公式为m = c^d mod n。由于d是e的乘法逆元，这一过程是可逆的，从而实现了加密和解密。 在实际应用中，RSA还常与其他算法（如AES）结合，用RSA加密AES的密钥，然后用AES加密大量数据，以平衡加密性能和安全性的需求。