数据降维实战：SVD与CUR方法详解

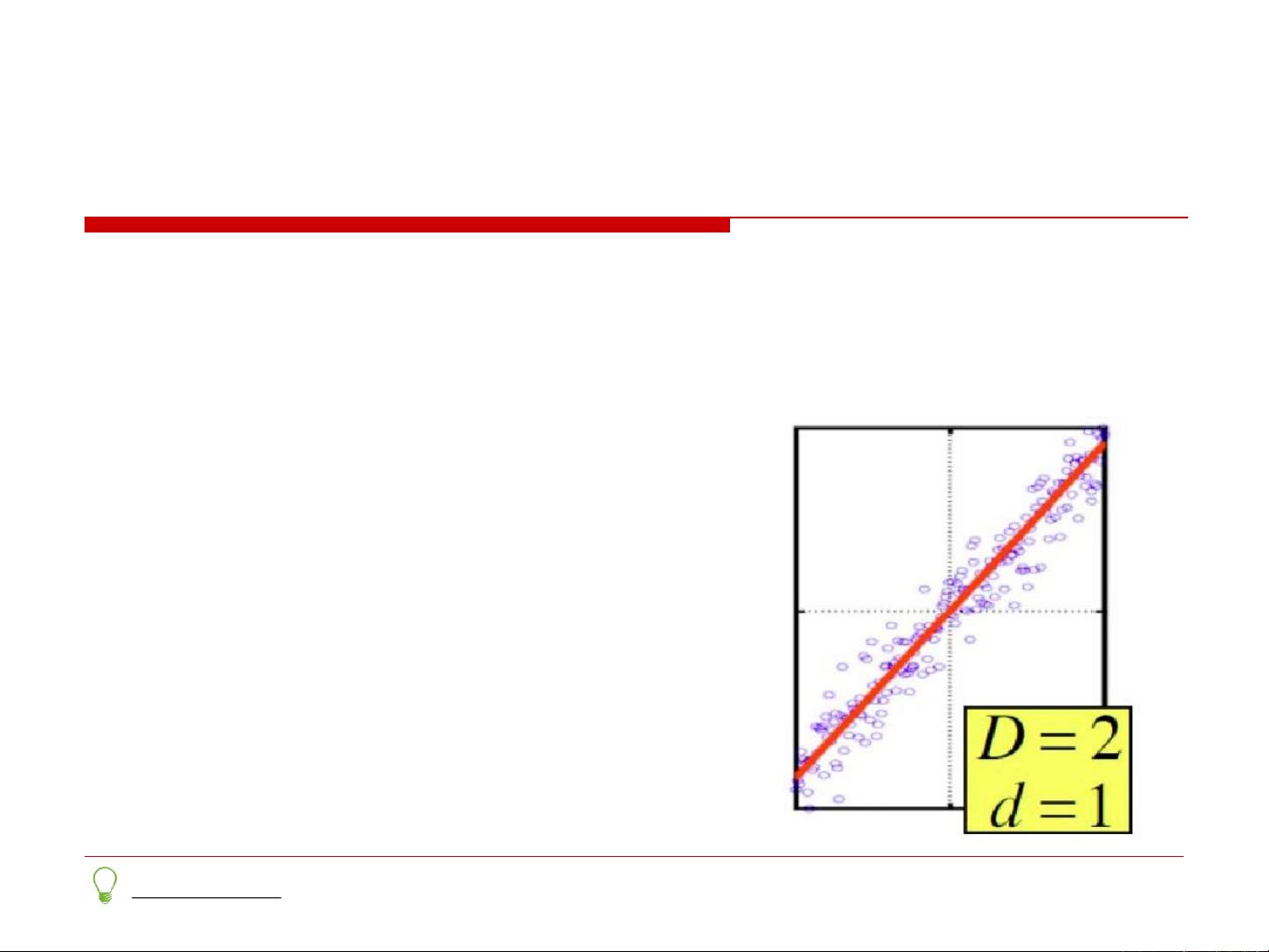
在七月的学习资料中，关于数据挖掘的课程特别关注了海量高维数据与维度约减这一主题，主要讲解了为什么要进行数据降维以及如何通过两种主要方法——Singular Value Decomposition (SVD) 和 CUR 进行降维。课程由龙龙老师在2016年7月23日的6月数据挖掘班中进行。 为什么要降维： 1. 高维数据带来的挑战：由于海量数据规模过大，处理起来计算复杂度高，且模型复杂度也随之增加，降维可以有效降低存储和计算成本。 2. 提升模型效率：降维使得模型更容易理解和维护，即使使用简单模型也能获得更好的性能。 3. 优化预测：通过降维，即使使用非最优模型和参数也能得到良好的预测效果，减少对最佳模型选择的依赖。 为什么能降维： 数据实际上可能在低维子空间中，并且子空间的坐标轴能够提供最有效的数据表示。这种假设基于数据的内在结构，即数据分布具有一定的规律性和低秩特性。 矩阵秩的重要性： - 矩阵的秩定义为线性独立列（或行）的数量，反映了矩阵的重要维度。 - 关心矩阵秩是因为它有助于理解矩阵的本质，并用于选择适当的基向量表示。 - 在降维过程中，秩相当于找到数据所需的最小维度。 SVD方法： - SVD是一种分解技术，将mxn的输入矩阵A分解为三个部分：左奇异向量矩阵U、奇异值矩阵∑和右奇异向量矩阵V的转置。 - U表示文章的主题分布，∑包含每个主题的重要性，V表示词与主题的关联程度。 - 通过SVD，可以将原始数据映射到低维空间，从而实现降维。 CUR方法： - CUR方法是另一种降维策略，它选取部分列（C）和行（U）来重构原始矩阵，适用于特定场景，如稀疏数据处理。 总结： 通过学习这些内容，学生掌握了数据降维的重要性，理解了SVD和CUR方法在处理高维数据时的理论基础和实际应用。理解矩阵秩的概念有助于找到数据在低维空间中的投影，从而简化数据处理，提高模型效率。这对于从事数据分析、机器学习或数据挖掘的人员来说，是提升工作效率和分析能力的关键知识点。