"数据结构哈夫曼树课件.ppt详解及构造方法"

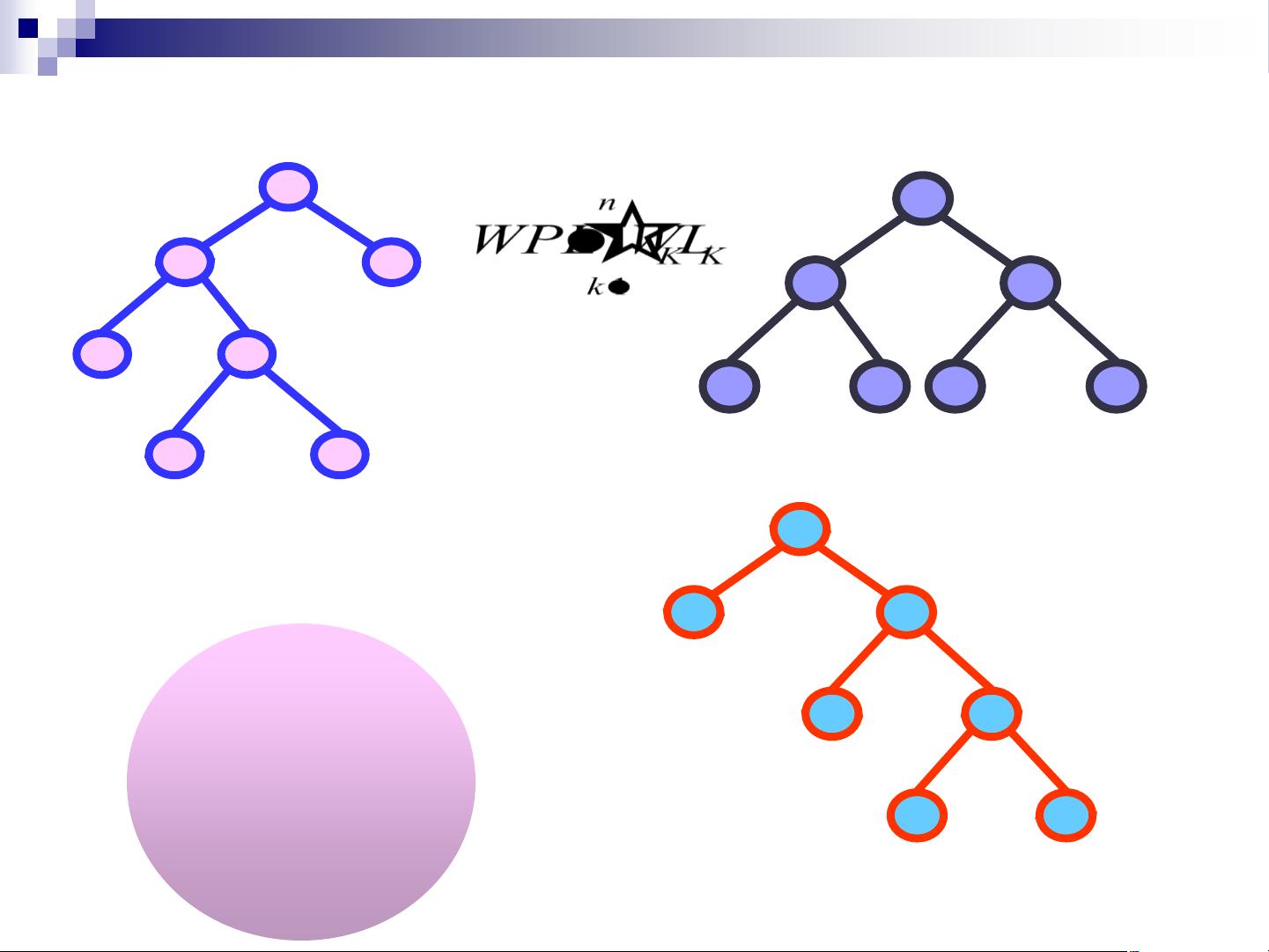
数据结构哈夫曼树是一种重要的树形结构，它在数据压缩和编码领域有着广泛的应用。哈夫曼树的构造和理论基础是数据结构课程中的重要内容，需要掌握其基本术语和构造方法。 在一棵树中，从一个结点往下可以达到的孩子或子孙结点之间的通路称为路径，通路中分支的数目称为路径长度。根据树的定义，树的路径长度规定为根结点到叶子结点之间的路径长度，而叶子结点的带权路径长度为叶子结点的权值与路径长度的乘积。树的带权路径长度则是所有叶子结点的带权路径长度之和。 在构造哈夫曼树时，需要首先定义哈夫曼树的基本术语。结点的权是树的结点附加的有着某种意义的实数，而带权路径长度则是从根结点到该结点之间的路径长度与该结点的权的乘积。构造哈夫曼树需要找到带权路径长度达到最小的二叉树，这样的二叉树称为最优二叉树，也称为哈夫曼树。构造哈夫曼树的过程中，需要首先确定树中的结点数目和各个结点的权值，然后根据权值构造出带权路径最小的哈夫曼树。 举例来说，如果有4个结点，权值分别为7，5，2，4，构造有4个叶子结点的哈夫曼树的过程为：首先选取权值最小的两个结点，进行合并得到新的结点，并将权值之和作为新结点的权值。然后再从剩下的结点中选取权值最小的两个结点进行合并，直至所有结点合并为一个完整的哈夫曼树为止。在这个过程中，需要不断地比较和合并权值最小的结点，直到构造出带权路径最小的哈夫曼树为止。 哈夫曼树的构造过程需要严格按照规定的步骤和方法进行，确保得到的哈夫曼树是带权路径最小的最优二叉树。掌握了哈夫曼树的基本术语和构造方法，可以更好地理解和应用数据结构中的哈夫曼树相关内容，为后续的学习和工作打下坚实的基础。因此，数据结构哈夫曼树的学习和掌握对于计算机科学和技术领域的专业人士来说至关重要。 总之，数据结构哈夫曼树是一种在数据压缩和编码中有着广泛应用的树形结构，它的构造和理论基础是数据结构课程中的重要内容。掌握了哈夫曼树的基本术语和构造方法，可以更好地理解和应用相关内容，为后续的学习和工作打下坚实的基础。数据结构哈夫曼树的学习和掌握对于计算机科学和技术领域的专业人士来说至关重要。