最优化理论：惩罚函数法与无约束极小化

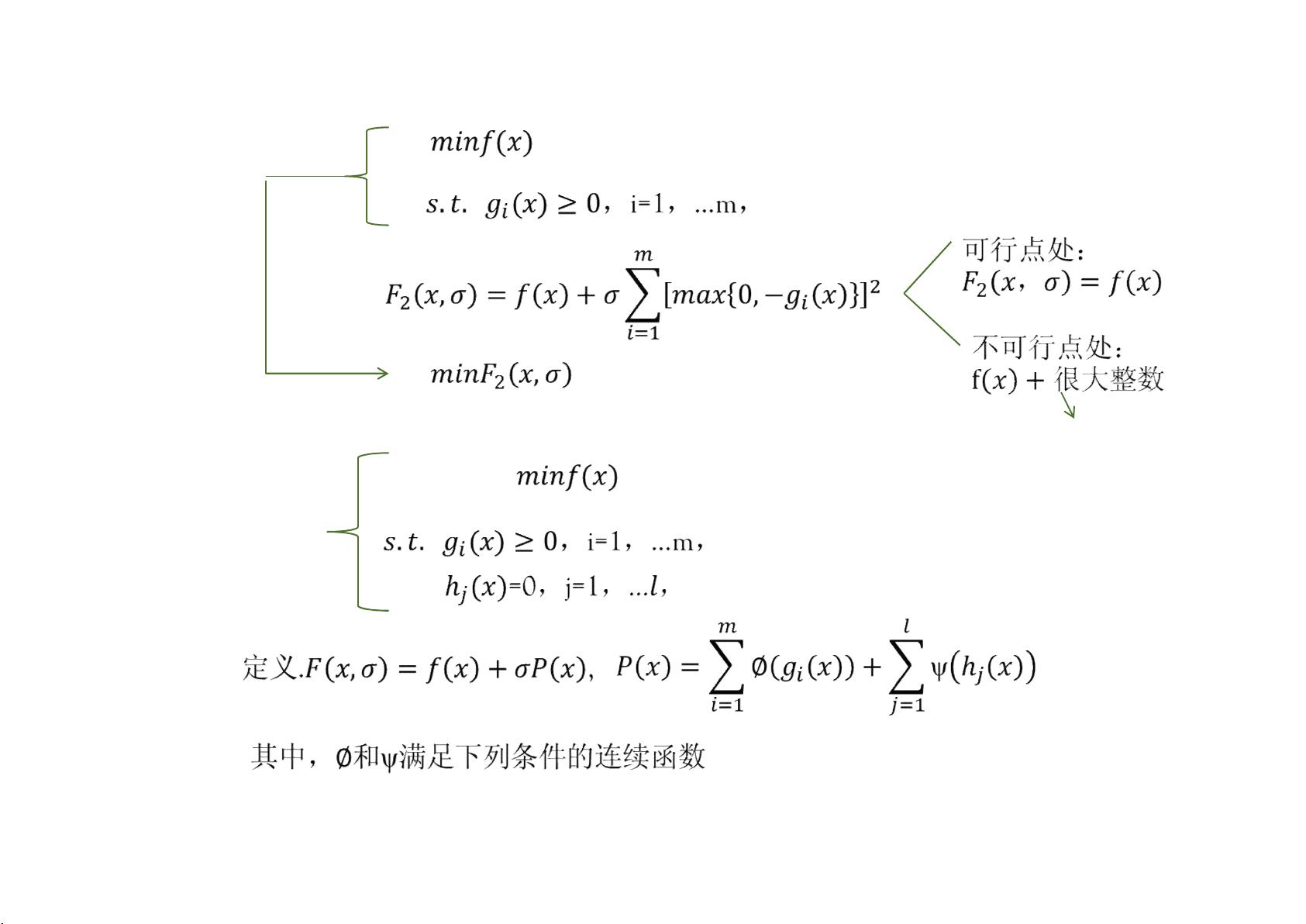
"最优化理论之惩罚函数法PDF讲义，深入浅出地讲解了如何利用惩罚函数法解决约束和无约束的最优化问题，包括外点罚函数法和内点罚函数法，并介绍了乘子法作为补充。" 在最优化理论中，惩罚函数法是一种有效的方法，用于处理带有约束条件的函数极值问题。它将约束条件通过引入惩罚项的方式纳入目标函数，使得在迭代过程中逐渐满足约束条件。这种方法既可以用于等式约束，也可以用于不等式约束。 1. 外点罚函数法 - 罚函数概念：当遇到等式约束时，可以通过消元处理转换，然后加入一个很大的正数项，使其在约束边界上得到极大惩罚。对于不等式约束，如果罚参数过大会导致计算困难，而过小则可能导致远离最优解。SUMT（Sequential Unconstrained Minimization Technique）方法是外点罚函数法的一种具体形式。 - 收敛性：外点法的收敛性由定理保证，随着罚参数的增加，解会趋向于原始问题的最优解。 2. 内点罚函数法 - 内点法从可行域内部开始搜索，尤其适用于处理不等式约束问题。它的关键是选择合适的罚参数r，过大可能导致解的不精确，过小则可能使问题变得病态，无法求解。 - 计算步骤包括逐步增大罚参数，以保证始终处于可行域内，最终达到优化目标。 3. 乘子法（Lagrange乘子法） - 乘子法由Hestenes和Powell提出，主要用于处理等式约束问题，通过引入Lagrange乘子来表达约束条件，寻找满足二阶充分条件的局部最优解。 - 对于不等式约束，乘子法会将问题转化为等式约束形式，利用增广Lagrange函数进行求解。 在实际应用中，可以借助MATLAB的optimization toolbox，如Quasi-Newton Method和Least-Squares Method，以及fmincon函数来实现这些优化算法。通过理解这些方法的原理和操作，可以有效地解决实际工程和科学问题中的最优化挑战。 总结来说，惩罚函数法及其变种如外点法和内点法，以及乘子法，是解决最优化问题的关键工具，它们提供了一套逐步逼近约束最优解的框架。理解并掌握这些方法，对于学习优化理论和解决实际问题至关重要。通过实践和编程，能够更深入地理解和应用这些理论。