奥数七大模块知识点详解与脑图概览

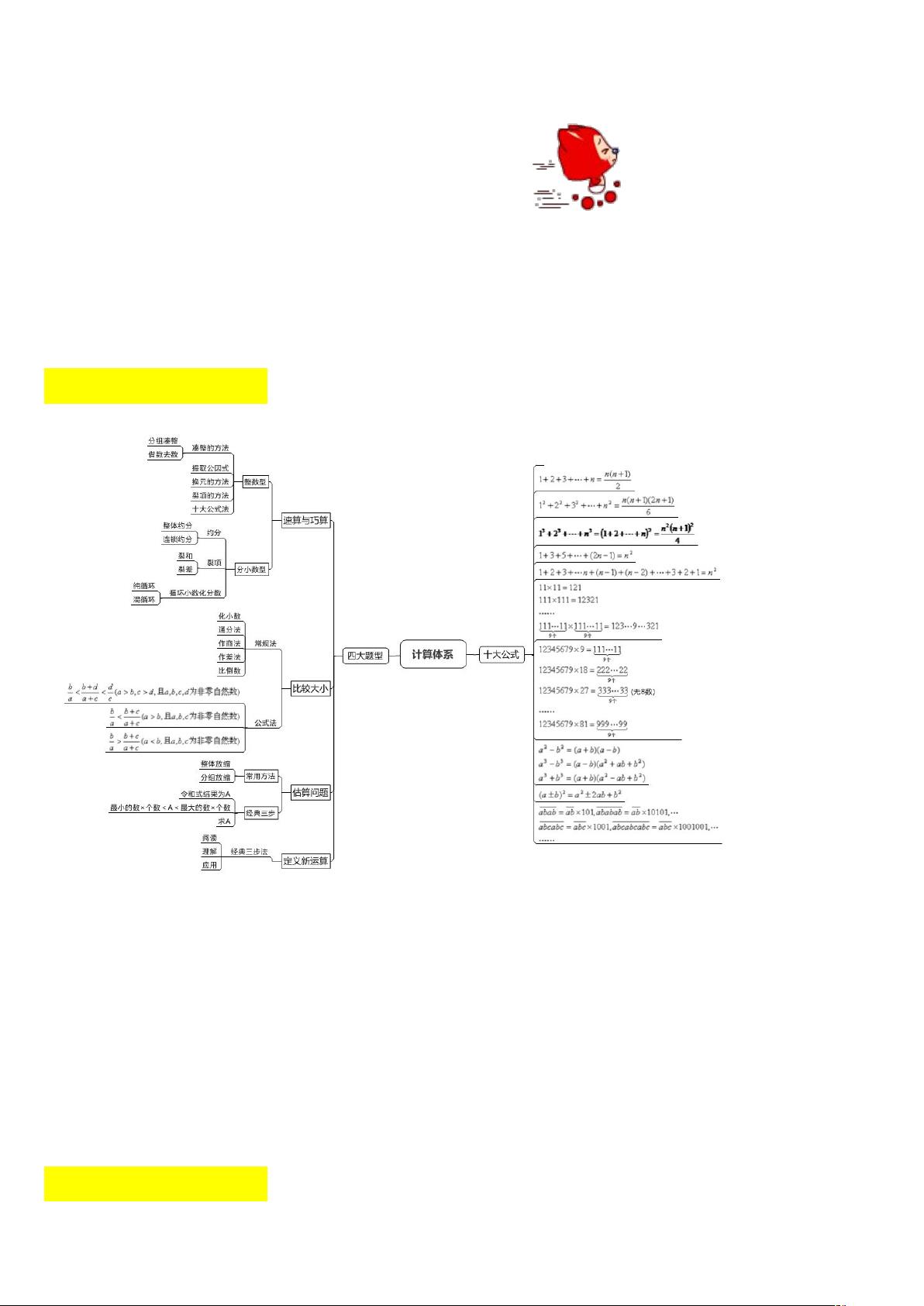
奥数作为数学思维的拓展，对小升初乃至更高层次的选拔考试具有重要意义。它主要由七大模块构成，分别是计算、数论、几何、行程、应用题、计数和杂题，这些模块涵盖了数学的各个方面，旨在考察学生的逻辑推理、问题解决和创新能力。 1. 计算模块：这部分着重训练学生的快速计算和巧妙运算能力，涉及速算技巧、分数小数混合运算、循环小数的转换、等差等比数列的理解，以及计算公式和特殊方法的应用，如裂项、换元和通项归纳。学生还需要掌握比较和估算技巧，以及定义新运算和解方程的能力。 2. 数论模块：这部分内容深入到数的性质和结构，包括质数与合数的辨识、因数倍数关系、整除的特性、位值原理、余数性质和同余问题等。中国剩余定理、完全平方数、奇偶性分析以及不定方程的解法也是重点。进制问题和最值问题则考验学生的抽象思维和策略运用。 3. 几何模块：分为直线型、曲线型和立体几何三个子领域。直线型几何关注长度、角度和图形变换，而曲线型涉及圆、扇形的周长与面积以及图形旋转问题。立体几何则探讨立体图形的表面积、体积计算，以及平面图形转化为立体模型的问题。 4. 行程模块：解决实际生活中的移动问题，如相遇、追击、环形跑道、流水行船、火车过桥、电梯和时间问题等，通过方程和比例法来求解，训练空间和时间观念。 5. 应用题模块：这部分强调将理论知识应用于实际情境，包括列方程解应用题、分数、百分数、比例、工程、浓度、经济和牛吃草等典型问题，培养学生解决实际问题的能力。 6. 计数模块：涵盖枚举法、分类法、加乘原理、排列组合、容斥原理、树形图表示等，通过计数技巧训练学生的逻辑推理和模式识别能力。 7. 杂题模块：这部分题目灵活多变，往往需要学生从简单情况出发，运用对应、转化、反面思考、染色覆盖、游戏策略等方法解决问题，培养创新和逆向思维能力。 学习奥数时，理解并掌握这些核心模块的关键知识点，能有效提升学生的数学素养和应对复杂问题的能力，为小升初考试和未来的学习打下坚实基础。同时，不断练习和应用这些知识点，是提高奥数水平的重要途径。