SIViP (2008) 2:141–153 143
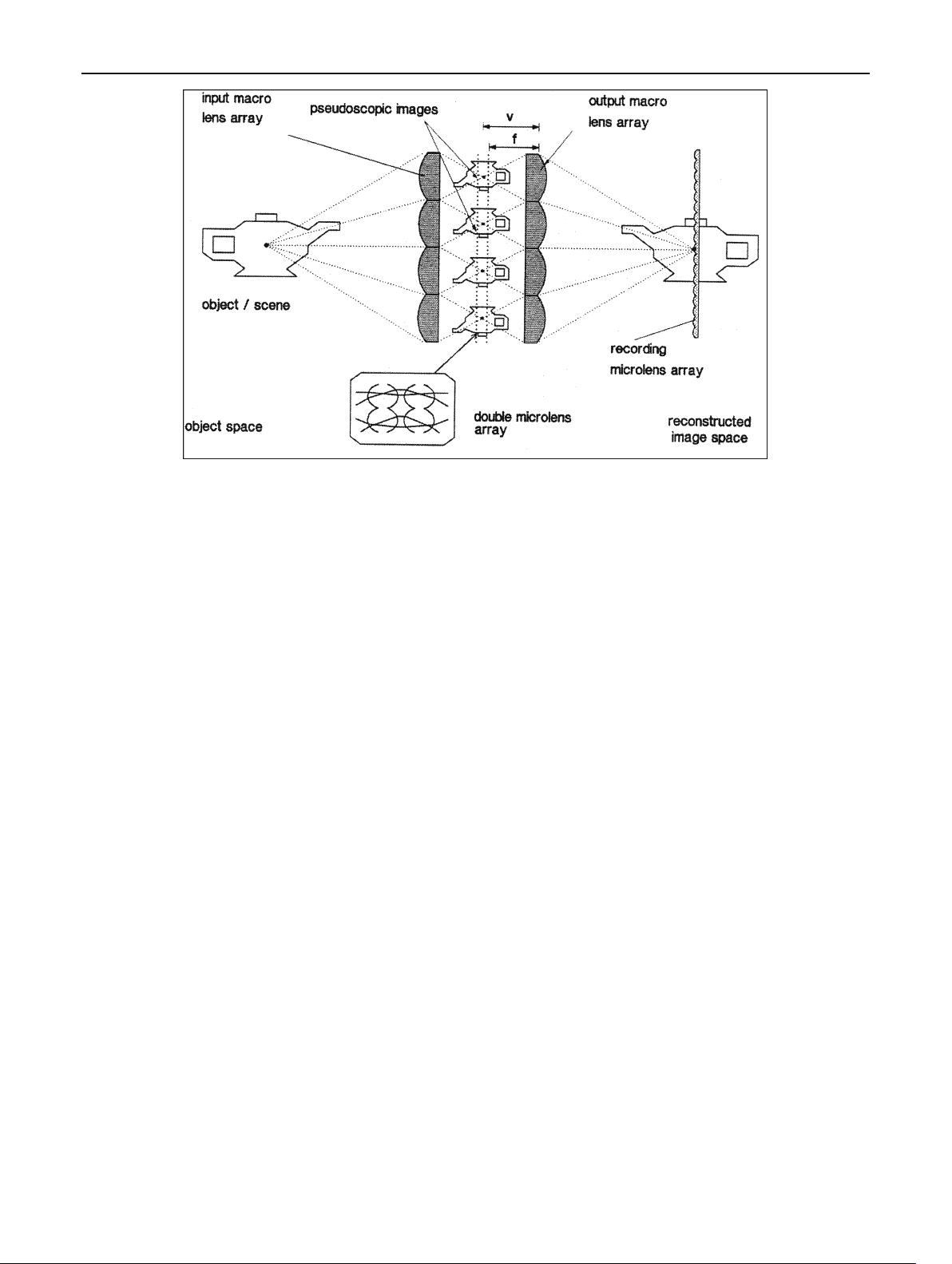
Fig. 1 Two tier optical network for transmission inversion optics
lenses and from Moiré interference patterns. More recently,
optical and digital techniques have been proposed to convert
the pseudoscopic image to an orthoscopic image [6–13].
The optical configuration necessary to record one stage
orthoscopic 3D integral images widely reported in literature
[6–8] and shown in Fig. 1 has been used for the capture of
the integral images used in this paper. This employs a pair
of microlens arrays placed back to back and separated by
their joint focal length, which produces spatial inversion. The
arrangement allows a pseudoscopic image to be transferred
such that it can straddle a separate microlens recording array.
The system uses an additional lens array, which images the
object space around the plane of the microlens combination.
This arrangement has been termed a two-tier optical com-
bination [6–8]. Effectively the first macro array produces a
number of pseudoscopic, laterally inverted, images around
the double integral microlens screen. This image is transmit-
ted effectively negating the sign of the input angle such that
each point in object space is returned to the same position in
image space. The arrangement performs pseudo phase conju-
gation, i.e. transfer of volumetric data in space. The image
is transmitted with equal lateral longitudinal magnification,
and the relative spatial co-ordinates, are preserved, i.e. there
is no inversion in the recorded image and no scale reduction
in depth.
It is possible to capture integral 3D images electronically
using a commercially available CCD array [6–8]. This form
of capture requires a high resolution CCD together with spe-
cialised optical components to record the micro-images fields
produced by precision micro-optics. The nature of CCD’s
will record live images in a regular block pixel pattern. The
planar intensity distribution representing an integral image
is comprised of 2D array of M × M micro-images due to
the structure of the microlens array used in the capture and
replay. The resulting 3D images are termed OII and have
parallax in all directions parallel to the capture plane. The
regular structure of the hexagonal microlenses array used in
the hexagonal grid gives rise to a regular ’brick structure‘ in
the intensity distribution as illustrated in Fig. 2.
Unidirectional integral images (UII) are obtained by using
a special case of the integral 3D imaging system where 1D
cylindrical microlens array is used for capture and replay
instead of a 2D array of microlenses. The resulting images
contain parallax in the horizontal direction only.
3 3D-DCT-compression model for OII data
A 3D-DCT-based compressionalgorithms which de-correlate
a group of adjacent micro-images from the source intensity
distribution data in both inter-micro-image and intra-micro-
image dimension simultaneously have been proposed [14–
17]. A group of (8 × 8) neighbouring micro-images from the
source intensity distribution, between which inter-band cor-
relation is high, is taken to form a (8×8× 8) volume of input
data for the 3D DCT. The algorithms have been extensively
applied on UII data.
More recently, a 3D-DCT-based OII encoder and decoder
has been proposed [17]. Due to the hexagonal microlenses
array used for capturing a 3D scene, the omni directional
integral sub-images form a “brick structure” arrangement as
shown in Fig. 2. The intensity distribution of the recorded 3D
123



































