加权双谱提升语音源噪声环境下DOA估计的鲁棒性

169 浏览量更新于2024-07-15 收藏 3.12MB PDF 举报

本文探讨的是加权双谱空间相关矩阵（Weighted Bispectrum Spatial Correlation Matrix, WBSCM）在语音源噪声鲁棒到达方向（Direction of Arrival, DOA）估计中的应用。传统的DOA估计在实际环境中面临的主要挑战之一是环境噪声，它可能来自多个方向或表现为非指向性噪声。为解决这一问题，研究者提出了一种创新性的方法，其核心在于利用双谱这一高级统计量（High Order Statistics, HOS）来增强鲁棒性。双谱是一种信号的第三阶统计特性，它提供了关于信号频率成分间相互关系的重要信息。WBSCM则是通过量化不同麦克风之间的双谱相位差（Bispectrum Phase Differences, BPD）的空间相关性，从而捕捉到噪声和语音信号在多通道设置中的关键区别。由于高斯噪声的HOS特性接近于零，将处理过程置于双谱域可以赋予该方法天然的抗噪声优势。此外，WBSCM中的BPD包含了与语音源DOA相关的冗余信息，这对于提升在非高斯噪声环境下的鲁棒性至关重要，特别是在存在定向干扰的情况下。通过选择合适的双谱加权策略，方法能够突出语音信号在DOA估计中的主导作用，这类似于信噪比优化过程，但针对的是双频谱特征。作者还设计了一种决策导向的双谱权重计算方法，以进一步优化估计性能。最后，他们基于WBSCM的特征值分析，提出了一种新的DOA估计器，这种估计器能够在复杂的噪声背景下提供更准确的方向定位。实验证明，这种方法在各种嘈杂环境中展现出显著的鲁棒性和有效性，特别是在处理高噪声和复杂声学场景时，WBSCM技术展现出了显著的性能提升。这项研究不仅扩展了DOA估计的传统方法，也为麦克风阵列信号处理领域提供了重要的理论支持和技术手段。

XUE et al.: NOISE ROBUST DIRECTION OF ARRIVAL ESTIMATION FOR SPEECH SOURCE WITH WBSCM839

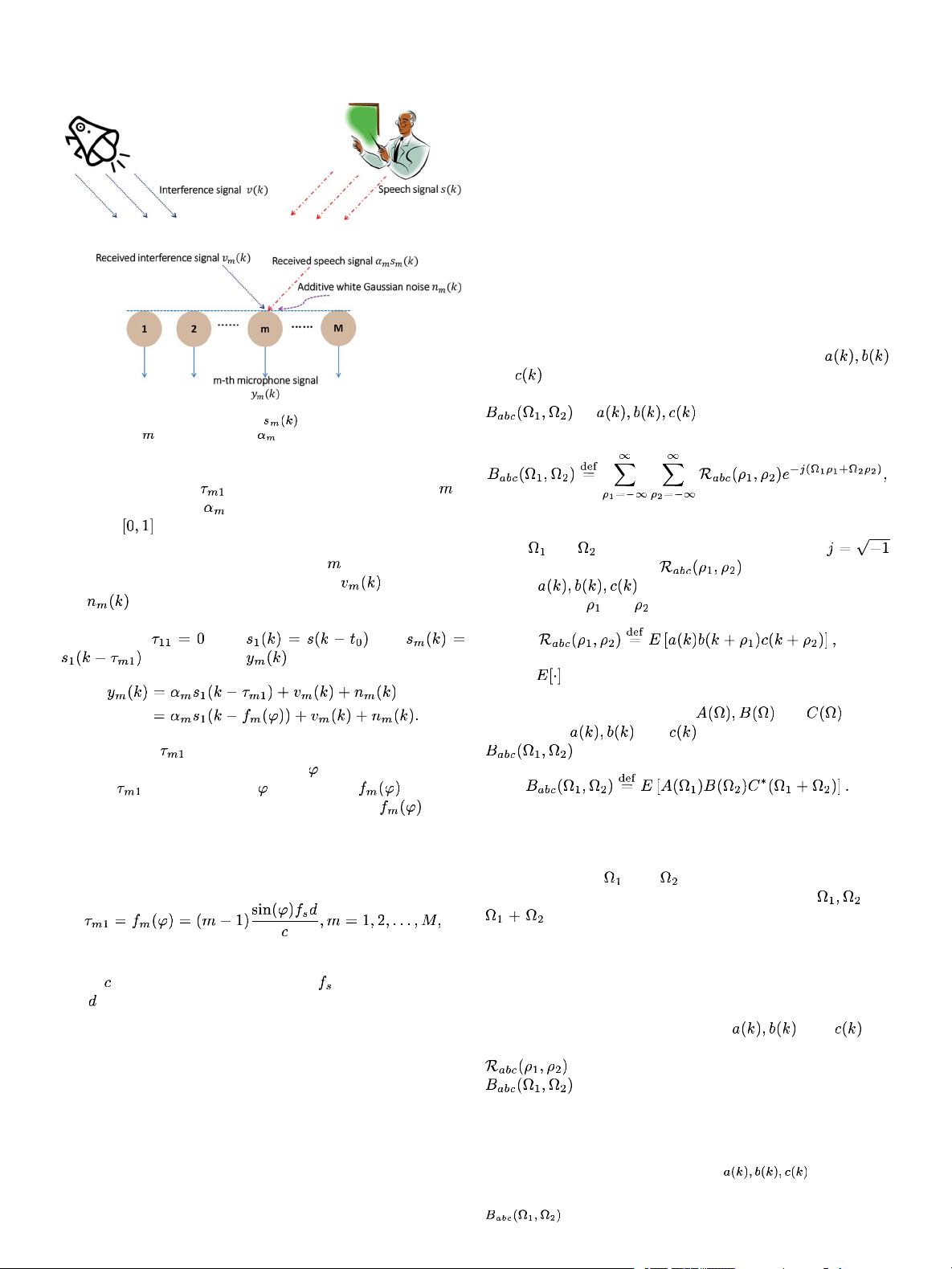
Fig. 1. Illustration of the signal model. is the unattenuated speech signal

received by the

th microphone, and is the attenuation factor. Other nota-

tions are described inside the ﬁgure.

ﬁrst microphone, and as the relative delay between the th

and ﬁrst microphone.

denotes the attenuation factor which

ranges in

. As only the speech signal which is related to the

DOA of speech source is of our interest, we ignore the details

of the interference signal received by the

th microphone, and

simply represent the interference signal as

. In addition,

the

stands for the additive zero-mean white Gaussian

noise.

Obviously,

,then ,and

. Consequently, can be rewritten as:

(2)

The time delay

is closely related to the geometry of the mi-

crophone array and real speech DOA

. If the array geometry

is ﬁxed,

depends only on ,thenweuse to denote

the dependency. The mathematical formulation of

can be

well deﬁned by geometrical computations. For example, a typ-

ical type of microphone array is the “uniform linear microphone

array (ULA),” in which the array elements are equispaced, and

in such case, we have:

(3)

where

is the speed of sound in the air, is the sampling rate,

and

is the spacing between two adjacent microphones.

III. P

HASE DIFFERENCE IN THE BISPECTRUM DOMAIN

A. Deﬁnitions and Properties of Bispectrum

In signal processing, one common way to describe the statis-

tical properties of stochastic processes is to use the measures of

second-order statistics, which generally include the auto-corre-

lation, cross-correlation, and the corresponding power spectrum

and cross-power spectrum. While the second-order statistics

are widely used in various ﬁelds of signal processing, these

measures only provide partial descriptions of the statistical

properties of stochastic processes [35]. Therefore, the princi-

ples of correlations and power spectra have been extended to

orders greater than two, and the concepts of HOS of stochastic

processes are then introduced [36]–[38]. HOS generally in-

clude the higher-order moment, higher-order cumulant and the

corresponding higher-order spectrum of stochastic processes.

The “bispectrum,” which is deﬁned in the order of three, is the

simplest higher-order spectrum. In the literature, for stationary

stochastic signals, analog to the deﬁnition of power spectrum,

the bispectrum is deﬁned as the 2-D Discrete Fourier Trans-

form (DFT) of the third-order cumulant of these stochastic

signals [39].

Now let us consider the bispectrum

of three zero-mean

stationary stochastic signals, which are denoted as

and . For zero-mean processes, the third-order cumulant

is identical to the third-order moment, then the bispectrum

of is deﬁned with the following

expression:

(4)

where

and are angular bi-frequency variables,

is the imaginary unit, and is the third-order mo-

ment of

, which is deﬁned depending on two in-

dependent lags

and :

(5)

where “

” is the expectation operator.

The bispectrum can also be deﬁned from another perspective

in terms of the signals' DFT. Let

and denote

the DFTs of

and , receptively. The bispectrum

is deﬁned as:

(6)

It can be derived that the deﬁnitions in (4) and (6) are

equivalent [39].

By deﬁnition, the bispectrum is a function of two bi-fre-

quency variables

and , and it analyzes the frequency

interactions between the frequency components at

and

where one frequency equals to the sum of the other

two. In [35], [39], [40], the properties of bispectrum (and other

HOS) have been discussed in great detail. Here, we simply

present two properties which will be useful for the analysis in

the following paper.

1) Property 1: If the probability density functions (PDFs)

of the zero-mean random processes

and are

all symmetrically distributed, then the third-order cumulant

equals to zero. According to (4), the bispectrum

also equals to zero.

The zero-mean Gaussian process is a typical kind of process

with symmetric PDF, then the bispectrum of zero-mean

In some literature, the authors call the deﬁnition in (4) as “cross-bispectrum,”

and the term “bispectrum” is used only when

are identical to

each other. In this paper, we view the “cross-bispectrum” as the generalized

deﬁnition of “bispectrum,” and for the sake of simplicity, we generally call

deﬁned in (4) as “bispectrum” unless mentioned.

剩余14页未读，继续阅读

weixin_38720461

粉丝: 9
资源: 923

加权双谱提升语音源噪声环境下DOA估计的鲁棒性

人工智能-语音识别-自动语音识别噪声鲁棒性方法研究.pdf

基础矩阵的鲁棒估计方法

gcc.rar_互相关 加权_加权时延_加权相关_加权谱估计_时延估计比较

什么是鲁棒DOA估计

在双基地MIMO雷达系统中，如何通过降维DOA矩阵技术准确估计信号源的角度，并确保在空间高斯色噪声与空间高斯白噪声背景下的鲁棒性？

语音识别模型噪声鲁棒性测试步骤

在双基地MIMO雷达系统中，降维DOA矩阵如何帮助实现相干源的角度估计？并且在空间高斯色噪声和空间高斯白噪声的复杂背景下，该技术如何保证角度估计的准确性与鲁棒性？

在三维点云数据处理中，如何结合IVCCS与加权双向距离ICP算法来提高噪声环境下的配准精度和鲁棒性？

加权music算法 matlab

如何结合IVCCS与加权双向距离ICP算法在噪声环境下提高三维点云配准的精度与鲁棒性？

最新资源

gcc.rar_互相关加权_加权时延_加权相关_加权谱估计_时延估计比较