分段函数解题指南：定义、性质与应用

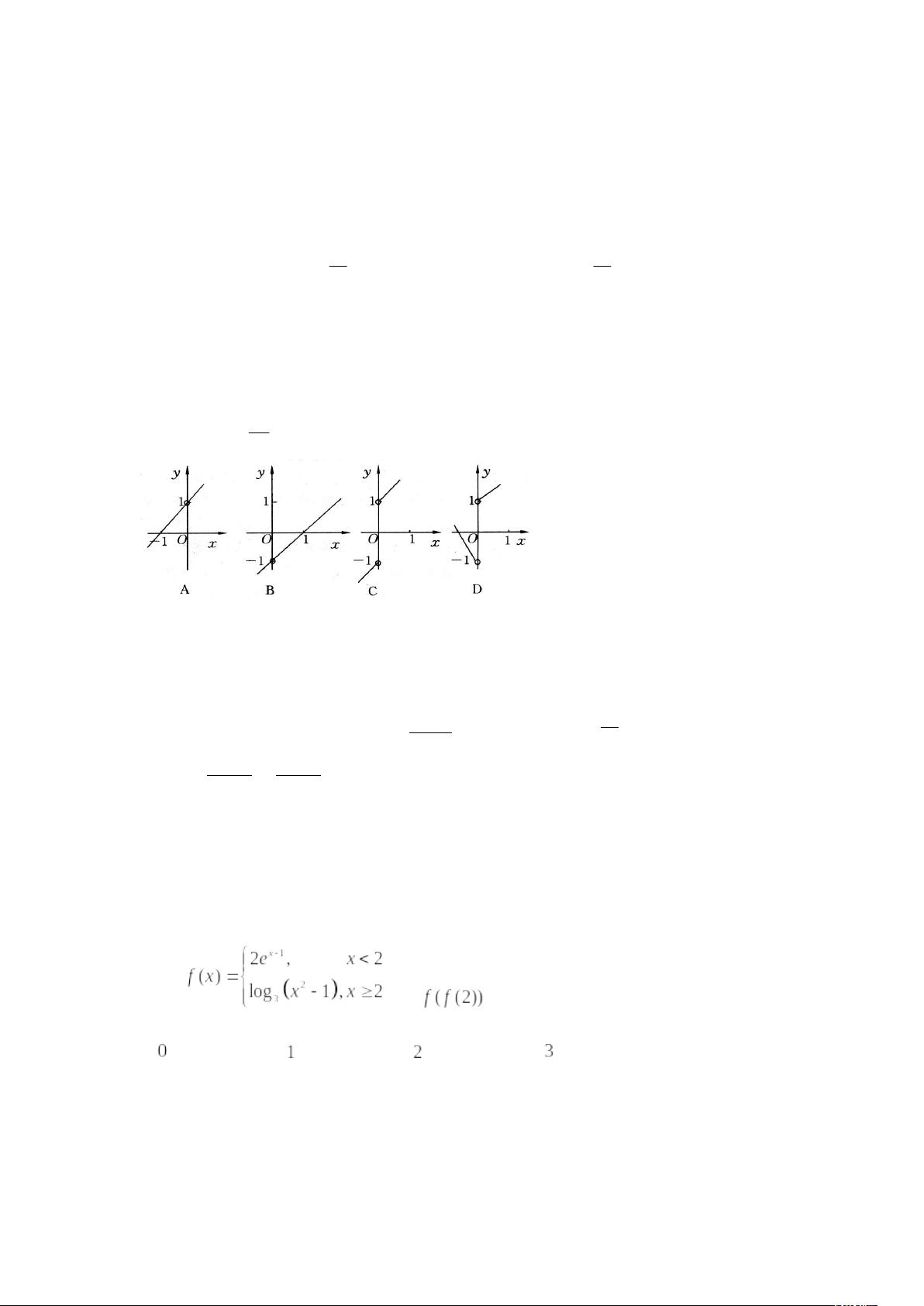
"分段函数相关的练习题及解析" 在数学中，分段函数是指一个函数在不同的定义域区间上有着不同的表达形式。这种函数通常在处理具有多种规则或特殊情况的问题时非常有用。以下是对给定文件中部分练习题的详细解释： 1. 题目要求求解分段函数的值。对于此类问题，关键在于确定输入值所对应的函数表达式。题目中0属于第二个表达式的定义域，-1属于第一个表达式的定义域，据此计算得到答案。 2. 这道题目考察的是根据分段函数的定义画出其图像。分段函数在不同的x值范围内有不同的解析式，因此需要分别画出每一段的图像，并结合在一起形成整体的函数图像。 3. 同一函数的判断标准是：定义域相同、值域相同以及对应关系一致。这里需比较每个选项中的函数在所有可能的x值上是否满足这三个条件，尤其注意分段函数的分段情况。 4. 此题同样涉及分段函数的求值，需要根据给定的x值选择正确的函数表达式进行计算，理解分段函数在不同区间上的行为是解答此类问题的关键。 5. 这个题目引入了递推关系，要求通过已知的分段函数关系求解特定值。利用递推关系，可以逐步计算出所需函数值。 6. 虽然也是求分段函数的值，但本题提示我们直接代入求解可能更为简便，避免了繁琐的作图过程。 7. 讨论分段函数的值域，需要分析每一段函数的值域，然后合并这些区间以得到整个函数的值域，这是解决这类问题的核心步骤。 8. 最后一道题涉及到不等式的解集，需要分析分段函数在a和-a处的函数值，根据题目给出的不等关系，找出a的可能取值范围。 这些练习题涵盖了分段函数的多个核心概念，包括求值、画图、比较函数是否相同、递推关系应用、值域求解以及不等式解集的确定。通过这样的练习，学生可以加深对分段函数的理解，提升处理复杂数学问题的能力。