计算机图形学：抛物线与三次样条曲线在CAD中的应用

"该资源是一份关于计算机图形学中抛物线及三次样条曲线的PPT，主要探讨了曲线在汽车设计、多媒体应用、飞机外形设计和计算机辅助设计（CAD）中的应用。通过对比传统设计方法和计算机辅助设计方法，强调了曲线理论在现代工业设计中的重要性。此外，还介绍了曲线的分类，包括规则曲线和不规则曲线，并讨论了如何用数学方法描述不规则曲线。" 计算机图形学中，曲线是至关重要的元素，它们在各种领域中有着广泛的应用。例如，在汽车制造业，设计师们使用曲线来创造流线型的车身设计，提高车辆的空气动力学性能和美学外观。B样条曲线是一种常用的工具，能够灵活地绘制出符合设计需求的汽车外形。抛物样条曲线则常用于绘制如鱼类等自然形态的物体，通过控制型值点来调整曲线形状，达到逼真的效果。 传统设计汽车的过程包括手绘车身草图、制作1:5模型、使用物理样条调整曲线，然后在绘图板上标注型值点并连接成光滑曲线。这种方法费时且易出错。相比之下，计算机辅助设计（CAD）通过三坐标测量仪获取精确数据，直接在计算机中进行处理，便于放大、修改和通过数控加工制造模型，大大提高了效率和准确性。 曲线和曲面的理论是CAD技术的基础，其发展与实际生产需求紧密相关。历史上，飞机和汽车制造商，以及科研机构投入大量资源研究曲线理论、表示方法和应用，推动了科技进步。例如，波音、通用汽车、雷诺和雪铁龙等公司在这方面做出了显著贡献。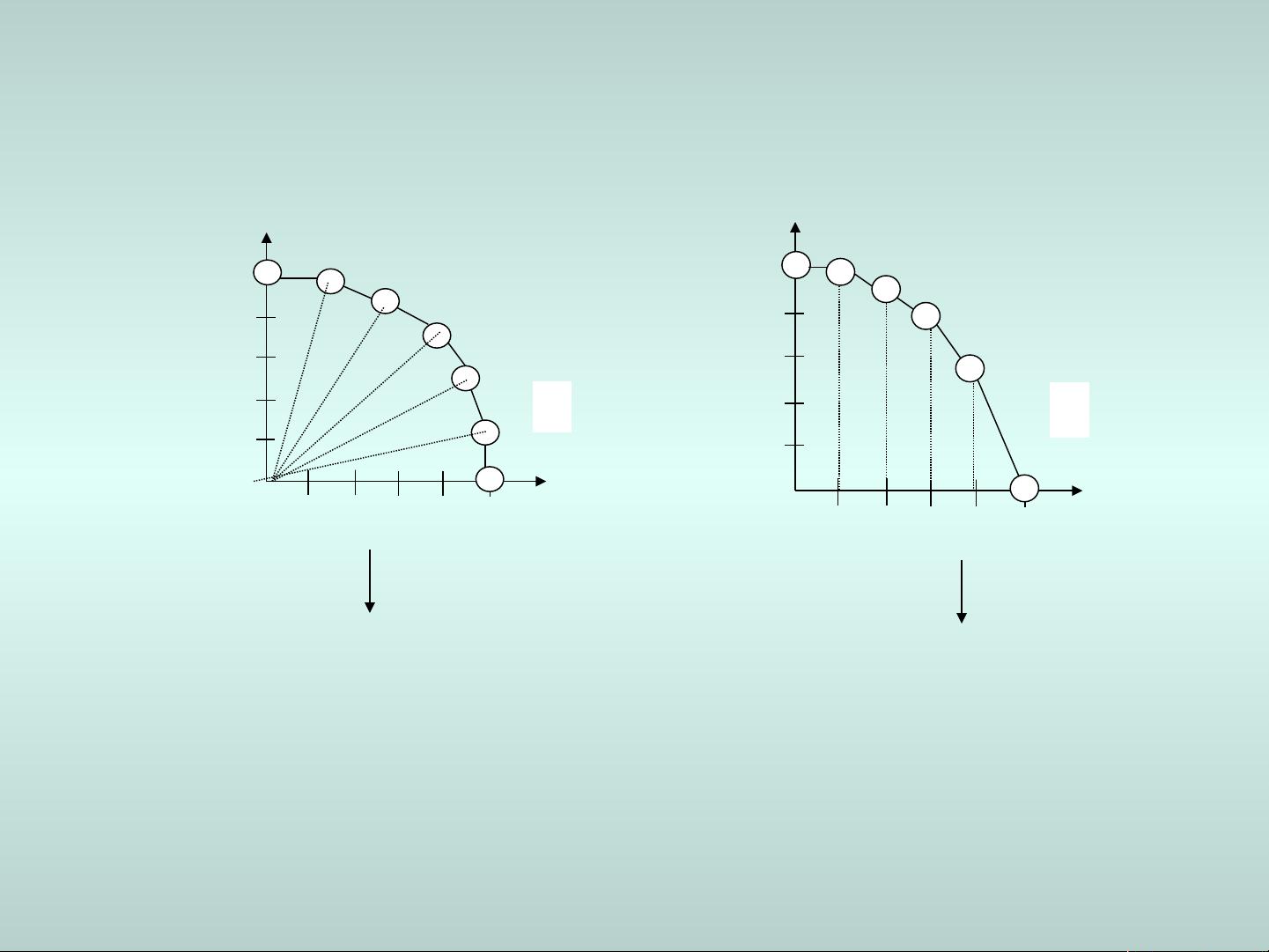 曲线通常分为两类：规则曲线和不规则曲线。规则曲线如圆、椭圆等，可以用标准的解析式表示；而不规则曲线，如统计曲线和实验曲线，由于数据点的离散性和不确定性，无法用单一的解析式描述。在这种情况下，数学方法如样条函数就被用来拟合这些离散点，构建出近似的连续曲线。 绘制曲线的方法多种多样，手工绘图中可能使用样条和压铁，而在计算机图形学中，可以通过数值方法、插值算法或参数化方法来实现。例如，对于不规则曲线，可以采用B样条或贝塞尔曲线，通过控制点来调整曲线形状，使其贴合给定的型值点。 计算机图形学中的抛物线和三次样条曲线是实现复杂形状建模的关键工具，尤其在汽车设计和工业造型中，它们扮演着不可或缺的角色。随着计算机技术的发展，曲线和曲面的理论将更加深入到各个领域，持续推动科技创新和设计效率的提升。