维纳滤波器详解及MATLAB仿真

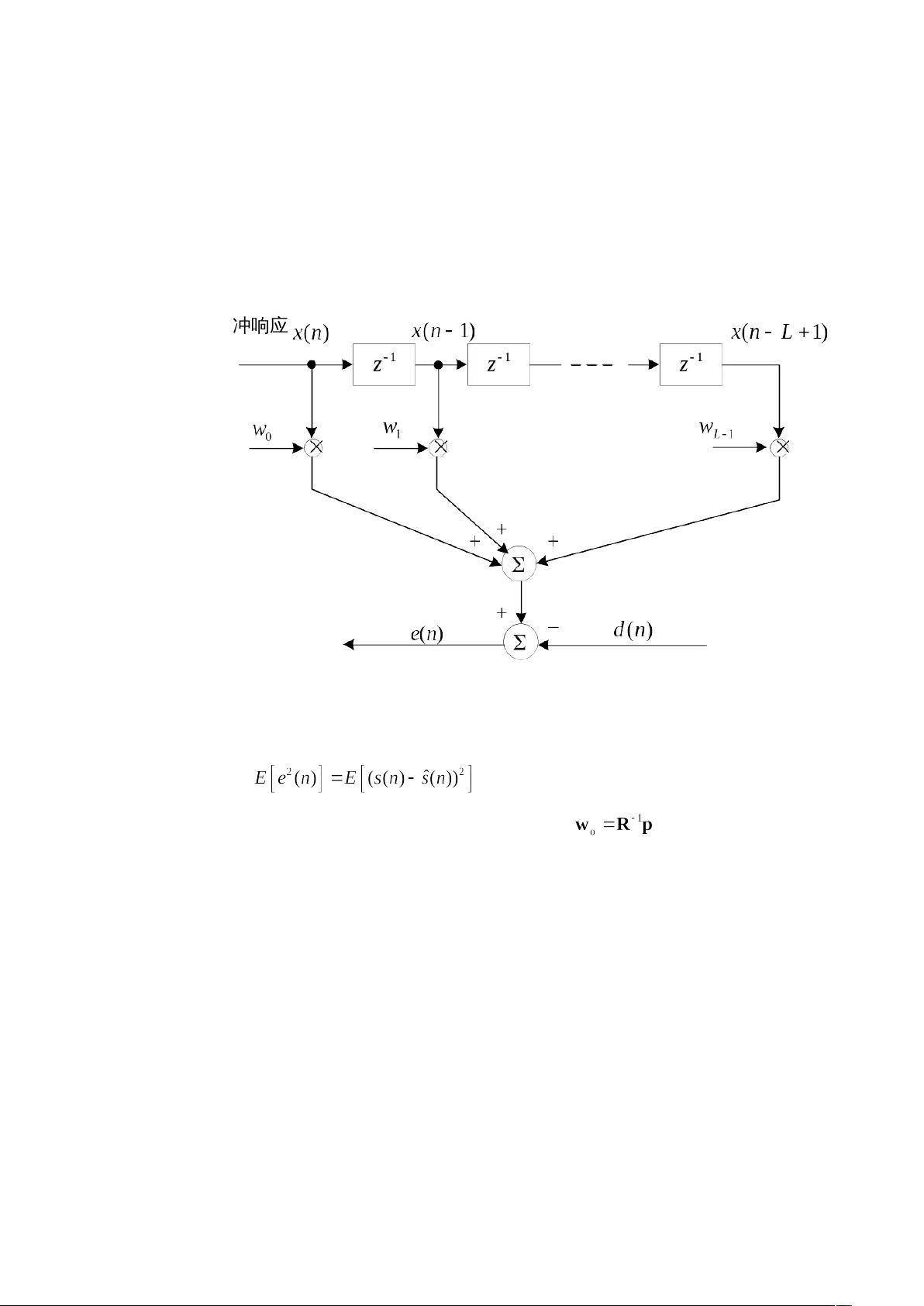
"维纳滤波器的设计与仿真是一个适合初学者学习的课题，主要涉及现代滤波理论，特别是如何处理信号与干扰频带重叠的情况。通过理解并应用维纳滤波器，可以实现对信号的最佳恢复，降低噪声的影响。" 维纳滤波器是一种基于最小均方误差准则的滤波技术，它不同于传统的滤波器，后者可能无法有效处理信号与噪声频谱重叠的情况。在现代滤波器中，维纳滤波器利用了信号和干扰的统计特性，如自相关函数和功率谱，来构建最优的估值算法。这个过程通常涉及到解决维纳-霍夫（Wiener-Hopf）方程。 在设计维纳滤波器时，目标是找到能够最小化均方误差的滤波器系数。这个误差是由滤波器输出与期望信号之间的差异造成的。维纳滤波器的解可以通过以下方式获得： 均方误差表达式为： \[ E = \min_{\mathbf{w}} \mathbf{e}^T \mathbf{e} \] 其中，\( \mathbf{e} \) 是误差向量，\( \mathbf{w} \) 是滤波器系数向量。在最小均方误差条件下，解满足维纳-霍夫方程： \[ \mathbf{w} = \mathbf{R}_{xx}^{-1} \mathbf{R}_{xy} \] 这里的 \( \mathbf{R}_{xx} \) 是含有噪声的混合信号的自相关矩阵，\( \mathbf{R}_{xy} \) 是混合信号与原信号的互相关向量。 在仿真过程中，首先需要生成信号和噪声。例如，通过产生随机高斯白噪声并将其添加到信号中，创建混合信号。然后计算混合信号的自相关函数 \( \mathbf{R}_{xx} \) 和混合信号与原信号的互相关函数 \( \mathbf{R}_{xy} \)。这些可以通过相关函数函数如 `xcorr` 来获取。接着，利用这些统计特性解出维纳滤波器的系数 \( \mathbf{h} \)，并通过卷积操作对混合信号进行滤波，从而恢复出更纯净的信号。 在给定的仿真程序代码中，可以看到这样的步骤： 1. 输入信号长度和滤波器阶数。 2. 生成随机高斯白噪声，并将其与原始信号相加，形成混合信号。 3. 计算混合信号的自相关矩阵 \( \mathbf{R}_{xx} \) 和混合信号与原信号的互相关向量 \( \mathbf{R}_{xy} \)。 4. 解维纳-霍夫方程，得到滤波器系数 \( \mathbf{h} \)。 5. 应用滤波器对混合信号进行滤波，得到滤波后的信号。 6. 绘制原始信号、含噪信号和滤波后信号的图形，以直观展示效果。 通过这样的仿真，初学者可以理解维纳滤波器的工作原理，掌握其设计与实现过程，进一步提升在信号处理领域的技能。