图论基础:无向图、有向图与连通性
需积分: 8 128 浏览量
更新于2024-07-01
收藏 697KB PPTX 举报
第六章的课程内容主要围绕图论的基本概念和性质展开,这是算法与数据结构课程中的重要组成部分。首先,章节开始定义了图的基本概念,指出图是一种非线性结构,其元素包括顶点(Vertex)和边(Edge)。在图G中,通常用V(G)表示顶点集,E(G)表示边集,形式上表示为G=(V,E)。
图根据边的方向性被分为三类:
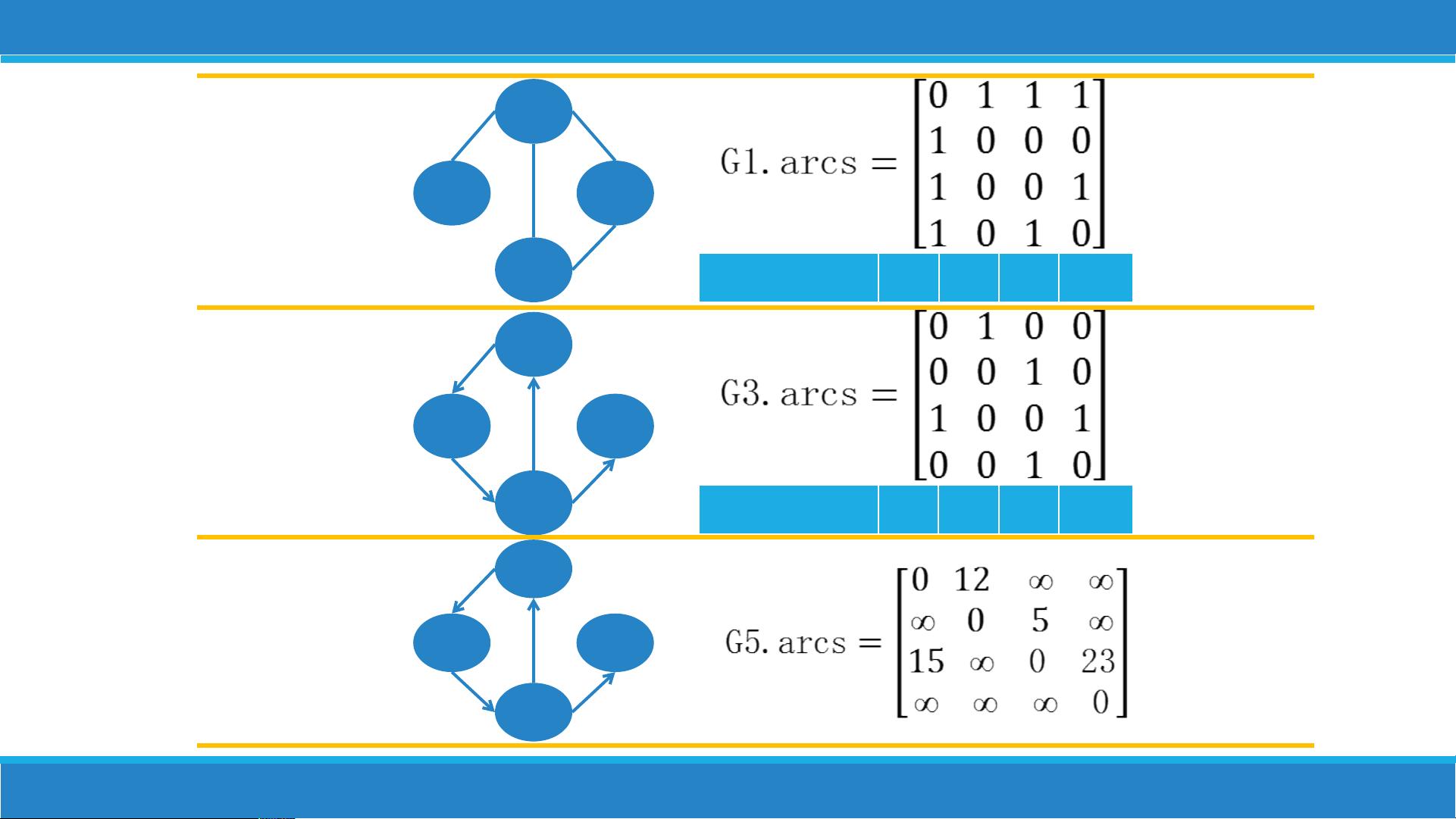
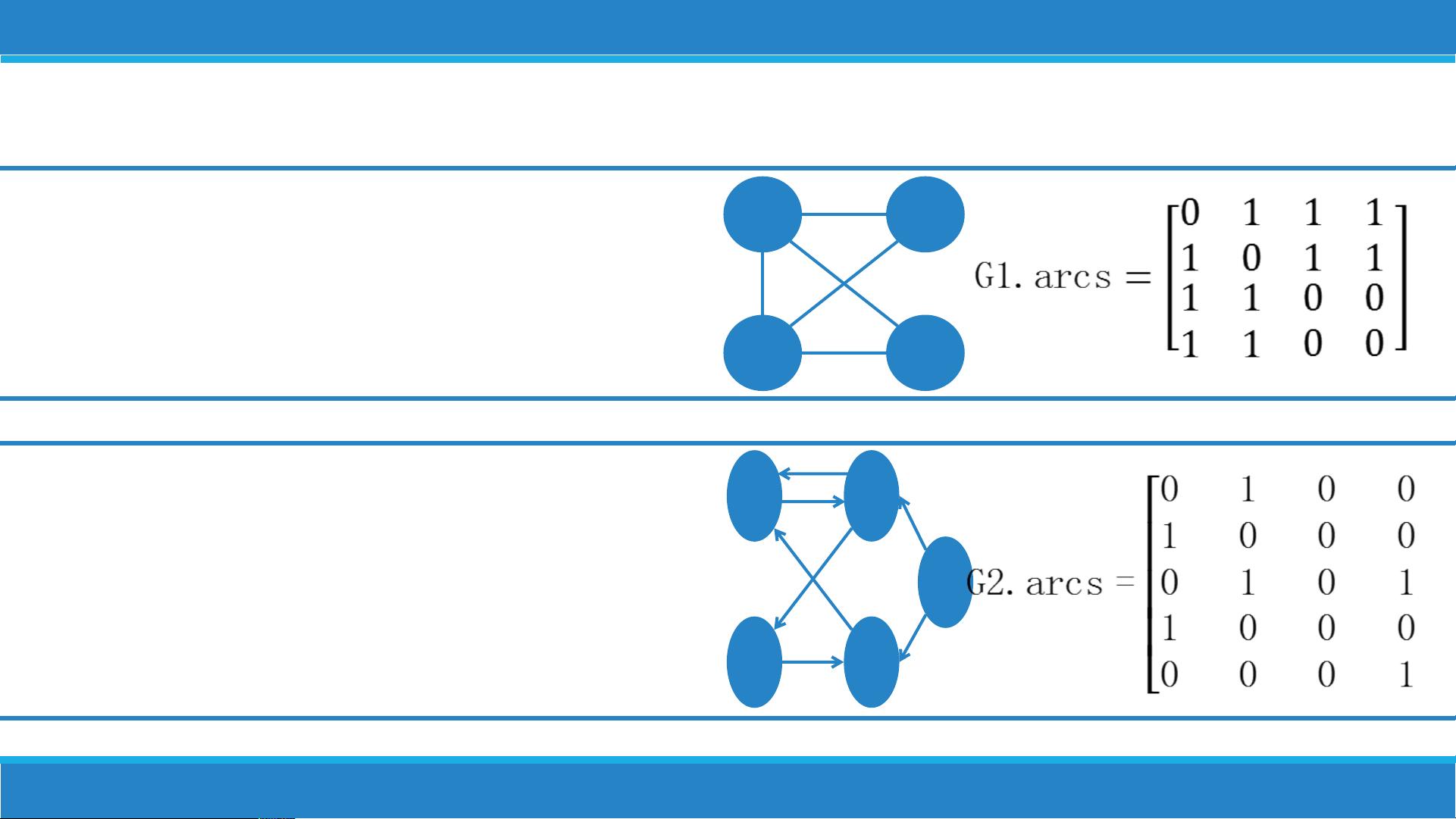
1. **无向图**:每条边没有方向性,例如(Vi, Vj)代表Vi和Vj之间的连接,无向完全图则是所有可能的顶点对之间恰好有一条边。
2. **有向图**:每条边都有方向,如<Vi, Vj>,表示从Vi到Vj的方向边,有向完全图的边数更多,允许双向连接。
3. **子图**:如果从一个更大的图G中取出一部分顶点和边,形成的新图G'称为原图的子图。
接下来,章节讨论了路径和回路的概念。简单路径指不重复经过除起点和终点外的顶点的路径,如ABDC;而简单回路则是起点和终点相同的简单路径,如ABDAV1V4V3V4V1。连通性是衡量图的重要特性,如果任意两点间有路径相连,则称图是连通的,连通图的极大连通子图被称为连通分量。在有向图中,强连通图意味着任意两个顶点之间既有从A到B的路径也有从B到A的路径,强连通分量是其特殊的连通分量。
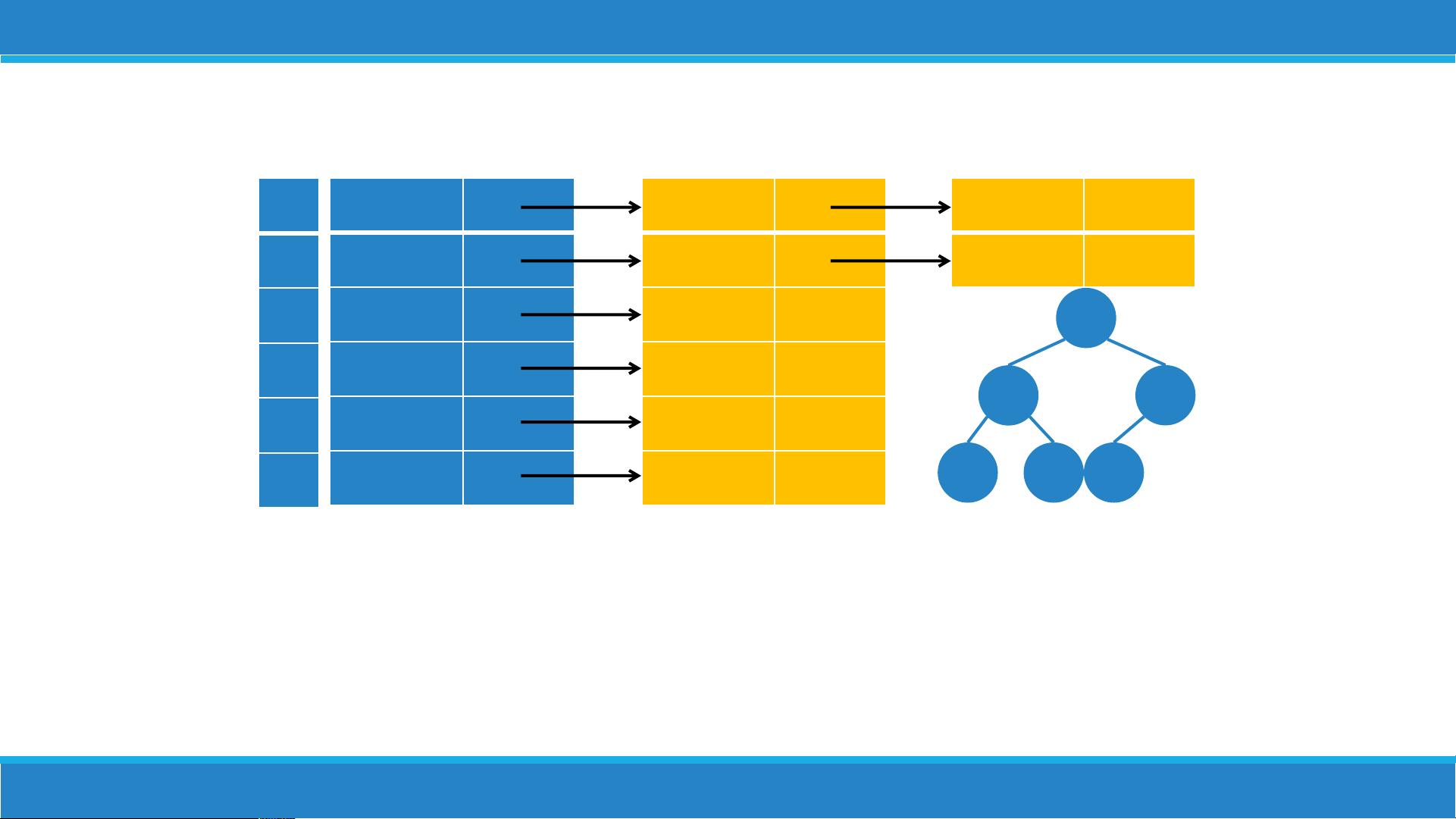
最后,章节引入了网络的概念,即带有权重的图,这种图常用于表示实际问题中的成本、距离等信息。提供了一些基本操作,如初始化图(InitGraph)、计算顶点的入度(indegree)和出度(outdegree),以及查找第一个邻居(firstNeighbour)等图的底层操作,这些都是算法设计和分析中必不可少的基础工具。
这一章节的内容涵盖了图论基础、图的分类、路径与连通性的概念,以及与实际应用相关的网络操作,对理解和实现许多数据结构和算法,如最短路径算法、拓扑排序等至关重要。学习者在深入理解这些概念后,能够更好地处理和分析复杂的数据关系,解决实际问题。
103 浏览量
2022-07-16 上传
604 浏览量
124 浏览量
119 浏览量
2008-03-15 上传
xishihai1977
- 粉丝: 0
- 资源: 14
最新资源
- robot_joint.tar.gz
- MT8-RGB程序更新 .zip
- Debouncer:Arduino的反跳库
- torch_sparse-0.6.4-cp36-cp36m-win_amd64whl.zip
- CourseSystem:C# 窗体应用程序,课程教务系统
- ngtrongtrung.github.io
- C20
- 技嘉B365M+9100F+5700XT(讯景雪狼版)
- flipendo-website:Flipendo 网站
- 智睿中小学校网站系统官方版源码 v3.3.0
- torch_sparse-0.6.7-cp37-cp37m-linux_x86_64whl.zip
- 取GB2312汉字.rar
- 纯CSS绿色下划线焦点的简洁导航
- 点文件:我的点文件
- fractals_py_p5:画出精美图片和曲线的五种方法称为分形
- 小学生噩梦--口算题卡生成器