0-1背包问题解析：动态规划与回溯法实现

"这篇文档详细介绍了0-1背包问题，这是一种经典的优化问题，涉及动态规划法和回溯法的解决方案。0-1背包问题要求在有限的背包容量下，选择物品以最大化总价值，每种物品只能选择0次或1次。文章提供了问题的数学描述，并阐述了动态规划算法的原理和设计步骤，以及该问题的应用背景和实际意义。" 0-1背包问题是一个经典的组合优化问题，出现在运筹学和计算机科学领域，由Dantzig在20世纪50年代提出。它的核心在于，在给定的背包容量限制下，我们需要从一系列物品中选择一部分，以最大化这些物品的总价值。每种物品有两种选择：要么完全放入背包，要么不放，不允许部分放入或者重复放入。 动态规划法是解决0-1背包问题的有效方法之一。这种算法的核心思想是通过构建一个表格来存储子问题的解，避免重复计算，从而提高效率。动态规划策略适用于具有最优化原理、无后向性和子问题重叠三个特性的问题。在0-1背包问题中，这意味着： 1. 最优化原理：最优解可以通过组合局部最优解得到。 2. 无后向性：每个阶段的选择不会影响之前阶段的状态。 3. 子问题重叠：许多子问题在不同阶段会重复出现。 设计动态规划算法的步骤包括： 1. 描述最优解的性质，比如背包问题中，最终的最优解包含的物品一定是每个子问题最优解的一部分。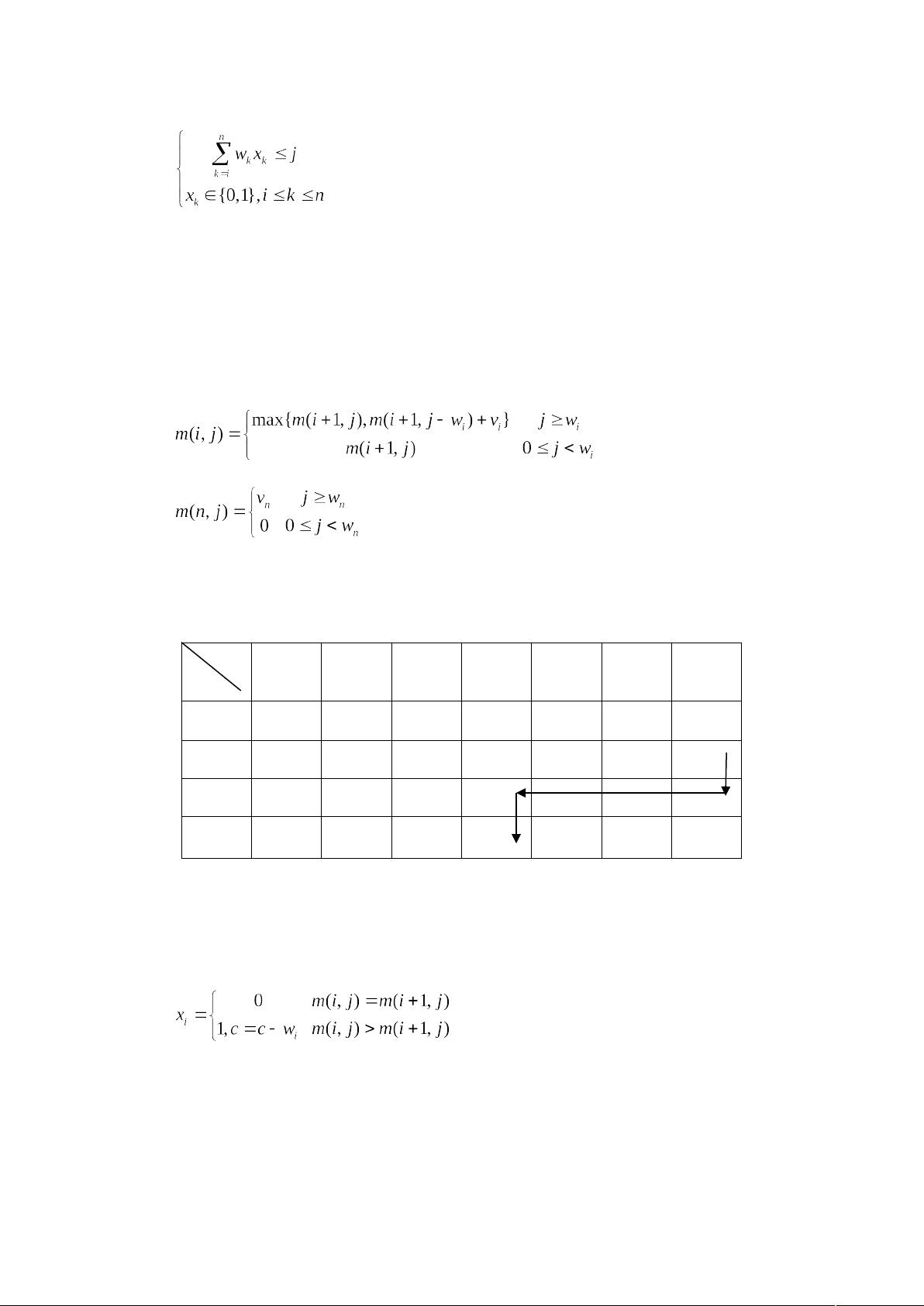 2. 递归定义最优值，对于0-1背包问题，这通常涉及到定义一个状态DP[i][j]表示前i个物品中选取总重量不超过j的部分所能获得的最大价值。 3. 自底向上计算最优值，通过填充DP表，从物品数量和容量的最小值开始，逐渐增加，直到处理完整个问题。 4. 通过回溯DP表的信息来构造最优解，例如，可以通过回溯表中每个状态的最大价值来源，确定哪些物品被选中。 此外，回溯法也是一种解决0-1背包问题的方法，它通过尝试所有可能的物品组合并回溯那些不符合条件的组合，但通常效率低于动态规划法。 0-1背包问题的实际应用广泛，涵盖了预算管理、项目选择、物流装载、材料切割等多个领域。由于其复杂性和广泛的实用性，它经常作为研究和教学的案例，同时也被用来解决更复杂的优化问题，例如整数规划问题。通过理解和掌握0-1背包问题的动态规划解决方案，可以为解决其他类似的优化问题提供基础。