机器人状态估计中的微李理论基础
需积分: 13 198 浏览量
更新于2024-07-15
收藏 1.51MB PDF 举报
"A micro Lie theory.pdf"
这篇文档主要探讨了李群和李代数在机器人领域中的应用，尤其关注它们在状态估计中的作用。李群和李代数是十九世纪数学家Sophus Lie提出的一种连续变换群的抽象理论，随着时间的发展，这一理论已经渗透到科学和技术的多个领域。在机器人学中，尤其是在导航系统的运动估计方面，近年来它们的应用呈现出显著增长的趋势。
然而，对于大多数机器人学者来说，李群理论高度抽象，理解起来颇具挑战性。文档指出，在机器人状态估计中，并不总是需要深入探究李群理论的所有细节，因此需要有选择地学习和应用相关知识。本文档旨在提供李群理论的基本原理，旨在清晰、实用地传达概念，同时舍弃了一些复杂的理论内容。
尽管进行了简化，但文档中包含的材料已被证明对现代机器人状态估计算法极其有用。这些基本概念包括但不限于：
1. 李群（Lie Group）：李群是一个集合，结合了群论（代数结构，如加法或乘法）和拓扑结构（连续性），使得群操作在空间内是连续进行的。在机器人学中，李群可以用来描述机器人的连续运动，如旋转和平移。
2. 李代数（Lie Algebra）：李群的导出结构，它提供了更简单的方式来分析和计算群的局部性质。在机器人学中，李代数通常用于线性化非线性问题，便于进行快速的动态和姿态估计。
3. 状态估计：在机器人导航中，状态估计是确定机器人位置、速度、姿态等关键参数的过程。李群和李代数提供了高级工具来融合来自各种传感器（如陀螺仪、加速度计、GPS）的数据，从而提高估计的准确性和鲁棒性。
4. 运动模型：李群和李代数可以帮助构建精确的机器人运动模型，这些模型可以捕捉到连续运动的细节，例如旋转和平移的组合。
5. 卡尔曼滤波与非线性优化：在状态估计算法中，李群理论可以用于改进经典的卡尔曼滤波器，通过李代数的线性化实现非线性问题的近似求解。此外，它还能应用于基于最小二乘的非线性优化问题，如滑动窗口优化（如EKF-SLAM）。
6. SLAM（Simultaneous Localization And Mapping）：在SLAM问题中，李群和李代数可以支持机器人在未知环境中同时建立地图并定位自身。通过有效的姿态估计，它们有助于减少累积误差，提高长期定位的精度。
通过理解和掌握这些基础知识，机器人工程师能够更好地设计和实现高效、稳健的导航系统。这份文档提供的简明教程将对那些希望深入研究机器人状态估计和控制理论的人提供宝贵的指导。
4
Table I
TYPICAL LIE GROUPS USED IN 2D AND 3D MOTION, INCLUDING THE TRIVIAL R
n
. SEE THE APPENDICES FOR FULL REFERENCE
Lie group M, ◦ size dim X ∈ M Constraint τ
∧
∈ m τ ∈ R
m
Exp(τ ) Comp. Action
n-D vector R
n
, + n n v ∈ R
n
v − v = 0 v ∈ R
n
v ∈ R
n
v = exp(v) v
1
+v
2
v + x
circle S
1
, · 2 1 z ∈ C z
∗
z = 1 iθ ∈ iR θ ∈ R z = exp(iθ) z
1
z
2
z x
Rotation SO(2), · 4 1 R R
>
R = I [θ]
×
∈ so(2) θ ∈ R R = exp([θ]
×
) R
1
R
2
R x
Rigid motion SE(2), · 9 3 M =
R t
0 1
R
>
R = I
h
[θ]
×
ρ
0 0
i
∈ se(2)
ρ
θ
∈ R
3
exp
h
[θ]
×
ρ
0 0
i
M
1
M
2
R x+t
3-sphere S
3
, 4 3 q ∈ H q
∗
q = 1 θ/2 ∈ H
p
θ ∈ R
3
q = exp(uθ/2) q
1
q
2
q x q
∗
Rotation SO(3), · 9 3 R R
>
R = I [θ]
×
∈ so(3) θ ∈ R
3
R = exp([θ]
×
) R
1
R
2
R x
Rigid motion SE(3), · 16 6 M =
R t
0 1
R
>
R = I
h
[θ]
×
ρ
0 0
i
∈ se(3)
ρ
θ
∈ R
6
exp
h
[θ]
×
ρ
0 0
i
M
1
M
2
R x+t
S
1
1
z(t)
T
1
S
1
= iR
T
z
S
1
z
v
^
= i! 2 iR
˙
z = z · i! /2 iR
1
v
^
= i! 2 iR
˙
z = i! 2 iR
!t
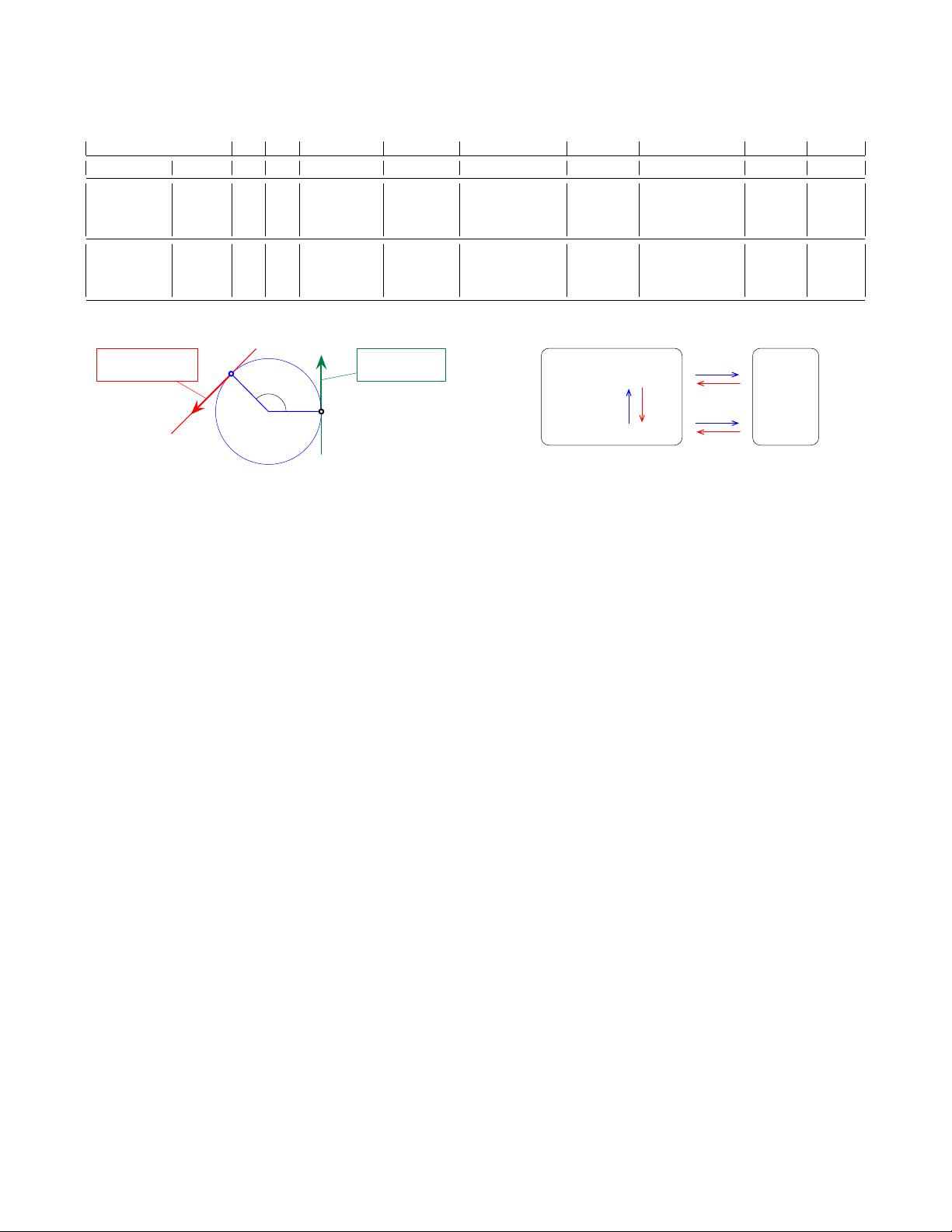
Figure 5. Let a point z ∈ S
1
move at constant rotation rate ω, z(t) =
cos ωt + i sin ωt. Its velocities when passing through 1 and z are in the
respective tangent spaces, T
1
S
1
and T
z
S
1
. In the case of T
z
S
1
, the velocity
is
˙
z = z iω = −ω sin ωt + iω cos ωt when expressed in the global
coordinates, and
z
v
∧
= iω when expressed locally. Their relation is given
by
z
v
∧
= z
−1
˙
z = z
∗
˙
z. In the case of T
1
S
1
, this relation is the identity
1
v
∧
=
˙
z = iω. Clearly, the structure of all tangent spaces is iR, which is
the Lie algebra. This is also the structure of
˙
z at the identity, and this is why
the Lie algebra is defined as the tangent space at the identity.
1) The Lie algebra m: The tangent space at the identity,
T
E
M, is called the Lie algebra of M, and noted m,
Lie algebra : m , T
E
M . (8)
Every Lie group has an associated Lie algebra. We relate the
Lie group with its Lie algebra through the following facts [5]
(see Figs. 1 and 6):
• The Lie algebra m is a vector space.
1
As such, its
elements can be identified with vectors in R
m
, whose
dimension m is the number of degrees of freedom of
M.
• The exponential map, exp : m → M, exactly converts
elements of the Lie algebra into elements of the group.
The log map is the inverse operation.
• Vectors of the tangent space at X can be transformed
to the tangent space at the identity E through a linear
transform. This transform is called the adjoint.
Lie algebras can be defined locally to a tangent point X,
establishing local coordinates for T
X
M (Fig. 5). We shall
denote elements of the Lie algebras with a ‘hat’ decorator,
such as v
∧
for velocities or τ
∧
= (vt)
∧
= v
∧
t for general
elements. A left superscript may also be added to specify the
precise tangent space, e.g.,
X
v
∧
∈ T
X
M and
E
v
∧
∈ T
E
M.
The structure of the Lie algebra can be found (see Ex-
amples 3 and 5) by time-differentiating the group constraint
1
In a Lie algebra, the vector space is endowed with a non-associative
product called the Lie bracket. In this work, we will not make use of it.
X 2 M
log
exp
Log
Exp
(·)
_
(·)
^
Manifold
⌧
^
2 m
Lie algebra
⌧ 2 R
m
Vector
Tangent
T
E
M
Figure 6. Mappings between the manifold M and the representations of its
tangent space at the origin T
E
M (Lie algebra m and Cartesian R
m
). Maps
hat (·)
∧
and vee (·)
∨
are the linear invertible maps or isomorphisms (10–11),
exp(·) and log(·) map the Lie algebra to/from the manifold, and Exp(·) and
Log(·) are shortcuts to map directly the vector space R
m
to/from M.
(3). For multiplicative groups this yields the new constraint
X
−1
˙
X +
˙
X
−1
X = 0, which applies to the elements tangent at
X (the term
˙
X
−1
is the derivative of the inverse). The elements
of the Lie algebra are therefore of the form,
2
v
∧
= X
−1
˙
X = −
˙
X
−1
X . (9)
2) The Cartesian vector space R
m
: The elements τ
∧
of
the Lie algebra have non-trivial structures (skew-symmetric
matrices, imaginary numbers, pure quaternions, see Table I)
but the key aspect for us is that they can be expressed as linear
combinations of some base elements E
i
, where E
i
are called
the generators of m (they are the derivatives of X around the
origin in the i-th direction). It is then handy to manipulate
just the coordinates as vectors in R
m
, which we shall note
simply τ . We may pass from m to R
m
and vice versa through
two mutually inverse linear maps or isomorphisms, commonly
called hat and vee (see Fig. 6),
Hat : R
m
→ m ; τ 7→ τ
∧
=
m
X
i=1
τ
i
E
i
(10)
Vee : m → R
m
; τ
∧
7→ (τ
∧
)
∨
= τ =
m
X
i=1
τ
i
e
i
, (11)
with e
i
the vectors of the base of R
m
(we have e
∧
i
= E
i
).
This means that m is isomorphic to the vector space R
m
—
one writes m
∼
=
R
m
, or τ
∧
∼
=
τ . Vectors τ ∈ R
m
are handier
for our purposes than their isomorphics τ
∧
∈ m, since they
can be stacked in larger state vectors, and more importantly,
2
For additive Lie groups the constraint X −X = 0 differentiates to
˙
X =
˙
X ,
that is, no constraint affects the tangent space. This means that the tangent
space is the same as the group space.
剩余16页未读，继续阅读
点击了解资源详情
点击了解资源详情
点击了解资源详情
2022-03-17 上传
2020-10-12 上传
2019-08-16 上传
2022-03-16 上传
2019-07-09 上传
2019-10-11 上传
soupbox
- 粉丝: 0
- 资源: 5
我的内容管理
展开
最新资源
- 深入浅出：自定义 Grunt 任务的实践指南
- 网络物理突变工具的多点路径规划实现与分析
- multifeed: 实现多作者间的超核心共享与同步技术
- C++商品交易系统实习项目详细要求
- macOS系统Python模块whl包安装教程
- 掌握fullstackJS：构建React框架与快速开发应用
- React-Purify: 实现React组件纯净方法的工具介绍
- deck.js：构建现代HTML演示的JavaScript库
- nunn：现代C++17实现的机器学习库开源项目
- Python安装包 Acquisition-4.12-cp35-cp35m-win_amd64.whl.zip 使用说明
- Amaranthus-tuberculatus基因组分析脚本集
- Ubuntu 12.04下Realtek RTL8821AE驱动的向后移植指南
- 掌握Jest环境下的最新jsdom功能
- CAGI Toolkit：开源Asterisk PBX的AGI应用开发
- MyDropDemo: 体验QGraphicsView的拖放功能
- 远程FPGA平台上的Quartus II17.1 LCD色块闪烁现象解析
